Prije razumijevanja B drvo i B+ drvo razlike, trebali bismo znati B stablo i B+ stablo odvojeno.
Što je B stablo?
B drvo je samo-balansirajuće stablo, i to je m-way stablo gdje m definira redoslijed stabla. Btree je generalizacija od Stablo binarnog pretraživanja u kojem čvor može imati više od jednog ključa i više od dva djeteta ovisno o vrijednosti m . U B stablu, podaci su specificirani sortiranim redoslijedom s nižim vrijednostima u lijevom podstablu i višim vrijednostima u desnom podstablu.
kako isključiti android način rada za razvojne programere
Svojstva B stabla
Sljedeća su svojstva B stabla:
- U B stablu svi lisni čvorovi moraju biti na istoj razini, dok u slučaju binarnog stabla lisni čvorovi mogu biti na različitim razinama.
Razumimo ovo svojstvo kroz primjer.
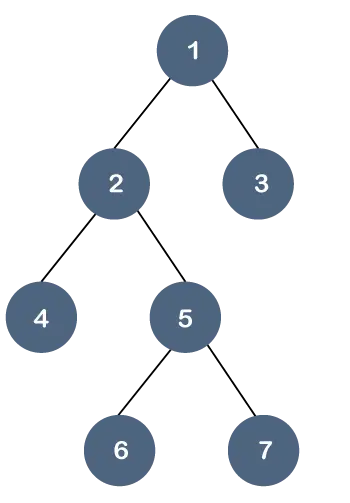
U gornjem stablu, svi lisni čvorovi nisu na istoj razini, ali imaju najviše dva djeteta. Stoga možemo reći da je gornje stablo a binarno stablo ali ne i B stablo.
- Ako Btree ima redoslijed m, tada svaki čvor može imati najviše m U slučaju minimalnih potomaka, lisnati čvorovi imaju nula djece, korijenski čvor ima dva djeteta, a unutarnji čvorovi imaju gornju granicu od m/2.
- Svaki čvor može imati najviše (m-1) ključeva. Na primjer, ako je vrijednost m 5, maksimalna vrijednost ključeva je 4.
- Korijenski čvor ima najmanje jedan ključ, dok svi ostali čvorovi osim korijenskog čvora imaju (gornja granica od m/2 minus - 1) minimalne ključeve.
- Ako izvodimo umetanje u B stablo, tada se čvor uvijek umeće u lisni čvor.
Pretpostavimo da želimo stvoriti B stablo reda 3 umetanjem vrijednosti od 1 do 10.
Korak 1: Prvo stvaramo čvor s 1 vrijednošću kao što je prikazano u nastavku:

Korak 2: Sljedeći element je 2, koji dolazi nakon 1 kao što je prikazano u nastavku:

Korak 3: Sljedeći element je 3 i umeće se nakon 2 kao što je prikazano u nastavku:

Kako znamo da svaki čvor može imati 2 maksimalna ključa, pa ćemo ovaj čvor podijeliti kroz srednji element. Srednji element je 2, pa se pomiče na svog roditelja. Čvor 2 nema nadređenog, pa će postati korijenski čvor kao što je prikazano u nastavku:

Korak 4: Sljedeći element je 4. Budući da je 4 veće od 2 i 3, bit će dodan nakon 3 kao što je prikazano u nastavku:

Korak 5: Sljedeći element je 5. Budući da je 5 veće od 2, 3 i 4, bit će dodan nakon 4 kao što je prikazano u nastavku:

Kako znamo da svaki čvor može imati 2 maksimalna ključa, pa ćemo ovaj čvor podijeliti kroz srednji element. Srednji element je 4, pa se pomiče na svog roditelja. Roditelj je čvor 2; stoga će se 4 dodati nakon 2 kao što je prikazano u nastavku:

Korak 6: Sljedeći element je 6. Budući da je 6 veće od 2, 4 i 5, 6 će doći nakon 5 kao što je prikazano u nastavku:

Korak 7: Sljedeći element je 7. Budući da je 7 veće od 2, 4, 5 i 6, 7 će doći nakon 6 kao što je prikazano u nastavku:

Kako znamo da svaki čvor može imati 2 maksimalna ključa, pa ćemo ovaj čvor podijeliti kroz srednji element. Srednji element je 6, pa se pomiče na svog roditelja kao što je prikazano u nastavku:

Ali, 6 se ne može dodati nakon 4 jer čvor može imati 2 maksimalna ključa, pa ćemo ovaj čvor podijeliti kroz srednji element. Srednji element je 4, pa se pomiče na svog roditelja. Kako čvor 4 nema roditelja, čvor 4 će postati korijenski čvor kao što je prikazano u nastavku:

Što je B+ stablo?
The B+ drvo također je poznato kao napredno samouravnoteženo stablo jer svaki put od korijena stabla do lista stabla ima istu duljinu. Ovdje ista duljina znači da se svi čvorovi lista pojavljuju na istoj razini. Neće se dogoditi da se neki od lisnih čvorova pojave na trećoj, a neki na drugoj razini.
Indeks stabla B+ smatra se indeksom više razina, ali struktura stabla B+ nije slična sekvencijalnim datotekama indeksa više razina.
Zašto se koristi B+ stablo?
B+ stablo se koristi za vrlo učinkovito pohranjivanje zapisa pohranjivanjem zapisa na indeksirani način korištenjem B+ stabla indeksirane strukture. Zahvaljujući višerazinskom indeksiranju, pristup podacima postaje brži i lakši.
B+ Struktura čvora stabla
Struktura čvorova B+ stabla sadrži pokazivače i ključne vrijednosti prikazane na donjoj slici:

Kao što možemo vidjeti u gornjoj B+ strukturi čvora stabla da sadrži n-1 ključnih vrijednosti (k1do kn-1) i n pokazivača (str1do strn).
Vrijednosti ključa za pretraživanje koje su smještene u čvor čuvaju se sortiranim redoslijedom. Dakle, ako i
Ograničenje na različite vrste čvorova
Neka je 'b' poredak B+ stabla.
Čvor koji nije list
Neka 'm' predstavlja broj djece čvora, tada se odnos između redoslijeda stabla i broja djece može predstaviti kao:

Neka k predstavlja vrijednosti ključa pretraživanja. Odnos između redoslijeda stabla i ključa pretraživanja može se predstaviti kao:
Kako znamo da je broj pokazivača jednak vrijednostima ključa pretraživanja plus 1, pa se matematički može napisati kao:
Broj pokazivača (ili djece) = broj tipki za pretraživanje + 1
Stoga bi maksimalan broj pokazivača bio 'b', a najmanji broj pokazivača bila bi gornja funkcija b/2.
Listni čvor
Listni čvor je čvor koji se pojavljuje na posljednjoj razini B+ stabla, a svaki listni čvor koristi samo jedan pokazivač za međusobno povezivanje kako bi se osigurao sekvencijalni pristup na razini lista.
U čvoru lista maksimalni broj djece je:

Maksimalni broj ključeva za pretraživanje je:
java niz sortiran

Korijenski čvor
Maksimalni broj djece u slučaju korijenskog čvora je: b
Minimalan broj djece je: 2
Posebni slučajevi u B+ stablu
1. slučaj: Ako je korijenski čvor jedini čvor u stablu. U ovom slučaju korijenski čvor postaje listni čvor.
U ovom slučaju, maksimalan broj djece je 1, tj. sam korijenski čvor, dok je najmanji broj djece b-1, što je isto kao i kod lisnog čvora.
Prikaz čvora lista u B+ stablu

Na gornjoj slici, '.' predstavlja pokazivač, dok su 10, 20 i 30 ključne vrijednosti. Pokazivač sadrži adresu na kojoj je pohranjena vrijednost ključa, kao što je prikazano na gornjoj slici.
Primjer B+ stabla

Na gornjoj slici čvor sadrži tri ključne vrijednosti, tj. 9, 16 i 25. Pokazivač koji se pojavljuje prije 9 sadrži ključne vrijednosti manje od 9 predstavljene s kja. Pokazivač koji se pojavljuje prije 16 sadrži ključne vrijednosti veće ili jednake 9, ali manje od 16 koje predstavlja kj. Pokazivač koji se pojavljuje prije 25 sadrži ključne vrijednosti veće ili jednake 16, ali manje od 25 predstavljene s kn.
Razlike između B stabla i B+ stabla

Sljedeće su razlike između B stabla i B+ stabla:
| B drvo | B+ drvo |
|---|---|
| U B stablu, svi ključevi i zapisi pohranjeni su u unutarnjim i lisnim čvorovima. | U B+ stablu, ključevi su indeksi pohranjeni u internim čvorovima, a zapisi su pohranjeni u lisnim čvorovima. |
| U stablu B ključevi se ne mogu više puta pohraniti, što znači da nema dupliciranja ključeva ili zapisa. | U B+ stablu može postojati redundancija u pojavljivanju ključeva. U ovom slučaju, zapisi su pohranjeni u lisnim čvorovima, dok su ključevi pohranjeni u unutarnjim čvorovima, tako da suvišni ključevi mogu biti prisutni u unutarnjim čvorovima. |
| U Btree-u, lisni čvorovi nisu međusobno povezani. | U B+ stablu, lisni čvorovi su međusobno povezani kako bi se osigurao sekvencijalni pristup. |
| U Btree-u pretraživanje nije vrlo učinkovito jer su zapisi pohranjeni u listovima ili internim čvorovima. | U B+ stablu pretraživanje je vrlo učinkovito ili brže jer su svi zapisi pohranjeni u lisnim čvorovima. |
| Brisanje internih čvorova je vrlo sporo i dugotrajan proces jer moramo uzeti u obzir i dijete izbrisanog ključa. | Brisanje u B+ stablu vrlo je brzo jer su svi zapisi pohranjeni u listovima čvorova tako da ne moramo uzeti u obzir dijete čvora. |
| U Btree-u sekvencijalni pristup nije moguć. | U B+ stablu, svi lisni čvorovi su međusobno povezani preko pokazivača, tako da je moguć sekvencijalni pristup. |
| U Btree-u se izvodi veći broj operacija cijepanja zbog čega se visina povećava u odnosu na širinu, | B+ drvo ima veću širinu u odnosu na visinu. |
| U Btreeju svaki čvor ima najmanje dvije grane i svaki čvor sadrži neke zapise, tako da ne moramo prelaziti do lisnih čvorova da bismo dobili podatke. | U B+ stablu unutarnji čvorovi sadrže samo pokazivače, a lisni čvorovi sadrže zapise. Svi lisni čvorovi su na istoj razini, tako da moramo prijeći do lisnih čvorova da bismo dobili podatke. |
| Korijenski čvor sadrži najmanje 2 do m djece gdje je m redoslijed stabla. | Korijenski čvor sadrži najmanje 2 do m djece gdje je m redoslijed stabla. |
