U ovom ćemo članku raspravljati o stablu binarnog pretraživanja. Ovaj će članak biti vrlo koristan i informativan studentima s tehničkim iskustvom jer je to važna tema njihovog kolegija.
Prije nego što prijeđemo izravno na stablo binarnog pretraživanja, prvo ćemo pogledati kratak opis stabla.
Što je drvo?
Stablo je vrsta strukture podataka koja se koristi za predstavljanje podataka u hijerarhijskom obliku. Može se definirati kao zbirka objekata ili entiteta koji se nazivaju čvorovi koji su međusobno povezani kako bi simulirali hijerarhiju. Stablo je nelinearna struktura podataka jer se podaci u stablu ne pohranjuju linearno ili sekvencijalno.
Sada započnimo temu, stablo binarnog pretraživanja.
Što je stablo binarnog pretraživanja?
Binarno stablo pretraživanja slijedi određeni redoslijed rasporeda elemenata. U stablu binarnog pretraživanja, vrijednost lijevog čvora mora biti manja od nadređenog čvora, a vrijednost desnog čvora mora biti veća od nadređenog čvora. Ovo se pravilo primjenjuje rekurzivno na lijevo i desno podstablo korijena.
Razumimo koncept stabla binarnog pretraživanja na primjeru.
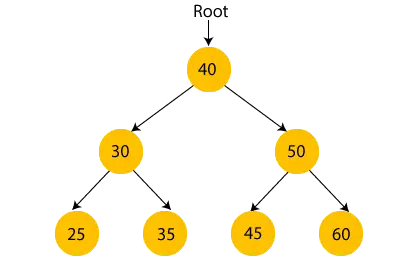
Na gornjoj slici možemo uočiti da je korijenski čvor 40, a svi čvorovi lijevog podstabla su manji od korijenskog čvora, a svi čvorovi desnog podstabla su veći od korijenskog čvora.
komponente robota
Slično, možemo vidjeti da je lijevi dijete korijenskog čvora veći od lijevog djeteta i manji od desnog djeteta. Dakle, također zadovoljava svojstvo binarnog stabla pretraživanja. Stoga možemo reći da je stablo na gornjoj slici binarno stablo pretraživanja.
Pretpostavimo da promijenimo vrijednost čvora 35 u 55 u gornjem stablu, provjerimo hoće li stablo biti binarno stablo pretraživanja ili ne.

U gornjem stablu, vrijednost korijenskog čvora je 40, što je veće od lijevog djeteta 30, ali manje od desnog djeteta 30, tj. 55. Dakle, gornje stablo ne zadovoljava svojstvo binarnog stabla pretraživanja. Stoga, gornje stablo nije binarno stablo pretraživanja.
Prednosti stabla binarnog pretraživanja
- Pretraživanje elementa u stablu binarnog pretraživanja jednostavno je jer uvijek imamo naznaku koje podstablo ima željeni element.
- U usporedbi s nizom i povezanim popisima, operacije umetanja i brisanja brže su u BST-u.
Primjer kreiranja stabla binarnog pretraživanja
Sada, pogledajmo stvaranje stabla binarnog pretraživanja koristeći primjer.
Pretpostavimo da su elementi podataka - 45, 15, 79, 90, 10, 55, 12, 20, 50
- Prvo, moramo umetnuti Četiri pet u stablo kao korijen stabla.
- Zatim pročitajte sljedeći element; ako je manji od korijenskog čvora, umetnite ga kao korijen lijevog podstabla i prijeđite na sljedeći element.
- Inače, ako je element veći od korijenskog čvora, umetnite ga kao korijen desnog podstabla.
Pogledajmo sada postupak stvaranja binarnog stabla pretraživanja pomoću zadanog elementa podataka. Proces stvaranja BST-a prikazan je u nastavku -
Korak 1 - umetnite 45.

Korak 2 - Umetnite 15.
Kako je 15 manje od 45, umetnite ga kao korijenski čvor lijevog podstabla.

Korak 3 - Umetnite 79.
Kako je 79 veće od 45, umetnite ga kao korijenski čvor desnog podstabla.

Korak 4 - Umetnite 90.
90 je veće od 45 i 79, pa će biti umetnuto kao desno podstablo od 79.

Korak 5 - umetnite 10.
10 je manji od 45 i 15, pa će biti umetnut kao lijevo podstablo od 15.

Korak 6 - Umetnite 55.
55 je veći od 45 i manji od 79, pa će biti umetnut kao lijevo podstablo od 79.

Korak 7 - Umetnite 12.
12 je manji od 45 i 15, ali veći od 10, pa će biti umetnut kao desno podstablo od 10.

Korak 8 - Umetnite 20.
20 je manji od 45, ali veći od 15, pa će biti umetnut kao desno podstablo od 15.

Korak 9 - Umetnite 50.
50 je veći od 45, ali manji od 79 i 55. Dakle, bit će umetnut kao lijevo podstablo od 55.

Sada je izrada stabla binarnog pretraživanja završena. Nakon toga, prijeđimo na operacije koje se mogu izvesti na binarnom stablu pretraživanja.
Možemo izvoditi operacije umetanja, brisanja i pretraživanja na stablu binarnog pretraživanja.
upravitelj zadataka za linux
Shvatimo kako se izvodi pretraživanje na stablu binarnog pretraživanja.
Pretraživanje u stablu binarnog pretraživanja
Pretraživanje znači pronaći ili locirati određeni element ili čvor u strukturi podataka. U stablu binarnog pretraživanja, pretraživanje čvora je jednostavno jer su elementi u BST-u pohranjeni u određenom redoslijedu. Koraci pretraživanja čvora u stablu binarnog pretraživanja navedeni su kako slijedi -
- Najprije usporedite element koji treba pretraživati s korijenskim elementom stabla.
- Ako se root podudara s ciljnim elementom, vraća lokaciju čvora.
- Ako se ne podudara, provjerite je li stavka manja od korijenskog elementa, ako je manja od korijenskog elementa, pomaknite se na lijevo podstablo.
- Ako je veći od korijenskog elementa, pomaknite se na desno podstablo.
- Ponovite gornju proceduru rekurzivno dok se ne pronađe podudaranje.
- Ako element nije pronađen ili nije prisutan u stablu, vratite NULL.
Razmotrimo sada pretraživanje u binarnom stablu koristeći primjer. Uzimamo binarno stablo pretraživanja formirano gore. Pretpostavimo da moramo pronaći čvor 20 s donjeg stabla.
Korak 1:

Korak 2:

3. korak:

Pogledajmo sada algoritam za pretraživanje elementa u stablu binarnog pretraživanja.
Algoritam za pretraživanje elementa u stablu binarnog pretraživanja
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Izlaz
Nakon izvršenja gornjeg koda, izlaz će biti -

Dakle, to je sve o članku. Nadamo se da će vam članak biti koristan i informativan.
