Što je Heap?
Hrpa je potpuno binarno stablo, a binarno stablo je stablo u kojem čvor može imati najviše dva djeteta. Prije nego saznate više o gomili Što je potpuno binarno stablo?
Potpuno binarno stablo je a binarno stablo u kojem sve razine osim zadnje razine, tj. lisnog čvora trebaju biti potpuno popunjene, a svi čvorovi poravnati lijevo.
Shvatimo kroz primjer.
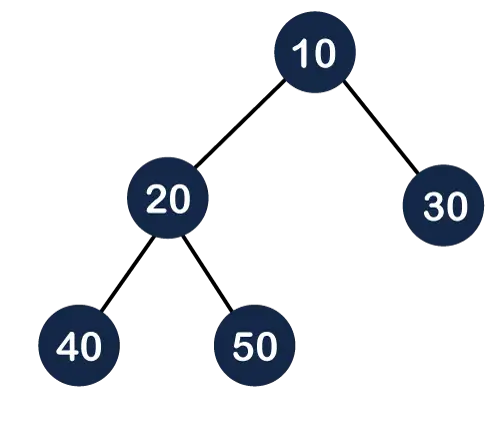
Na gornjoj slici možemo primijetiti da su svi unutarnji čvorovi potpuno ispunjeni osim lisnog čvora; stoga možemo reći da je gornje stablo potpuno binarno stablo.

Gornja slika pokazuje da su svi unutarnji čvorovi potpuno popunjeni osim lisnog čvora, ali lisni čvorovi dodani su na desnom dijelu; stoga, gornje stablo nije potpuno binarno stablo.
visina pomaka
Napomena: Heap stablo je posebna uravnotežena struktura podataka binarnog stabla gdje se korijenski čvor uspoređuje sa svojom djecom i raspoređuje u skladu s tim.
Kako možemo rasporediti čvorove u stablu?
Postoje dvije vrste hrpe:
- Min. gomila
- Maksimalna hrpa
Min. gomila: Vrijednost nadređenog čvora treba biti manja ili jednaka bilo kojem od njegovih potomaka.
Ili
Drugim riječima, min-hop se može definirati kao, za svaki čvor i, vrijednost čvora i je veća ili jednaka njegovoj nadređenoj vrijednosti osim korijenskog čvora. Matematički se može definirati kao:
[Roditelj(i)]<= a[i]< strong>
Razmotrimo min-heap kroz primjer.

Na gornjoj slici, 11 je korijenski čvor, a vrijednost korijenskog čvora manja je od vrijednosti svih ostalih čvorova (lijevo dijete ili desno dijete).
Maksimalna gomila: Vrijednost nadređenog čvora veća je od ili jednaka njegovim podređenim čvorovima.
Ili
Drugim riječima, max heap se može definirati kao za svaki čvor i; vrijednost čvora i manja je ili jednaka njegovoj nadređenoj vrijednosti osim korijenskog čvora. Matematički se može definirati kao:
A[Parent(i)] >= A[i]

Gornje stablo je stablo maksimalne hrpe jer zadovoljava svojstvo maksimalne hrpe. Sada, da vidimo prikaz niza maksimalne gomile.
Vremenska složenost u Max Heapu
Ukupan broj usporedbi potrebnih u maksimalnoj hrpi je prema visini stabla. Visina kompletnog binarnog stabla je uvijek logn; stoga bi vremenska složenost također bila O(logn).
Algoritam operacije umetanja u max heap.
// algorithm to insert an element in the max heap. insertHeap(A, n, value) { n=n+1; // n is incremented to insert the new element A[n]=value; // assign new value at the nth position i = n; // assign the value of n to i // loop will be executed until i becomes 1. while(i>1) { parent= floor value of i/2; // Calculating the floor value of i/2 // Condition to check whether the value of parent is less than the given node or not if(A[parent] <a[i]) { swap(a[parent], a[i]); i="parent;" } else return; < pre> <p> <strong>Let's understand the max heap through an example</strong> .</p> <p>In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.</p> <p> <strong>Insertion in the Heap tree</strong> </p> <p> <strong>44, 33, 77, 11, 55, 88, 66</strong> </p> <p>Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:</p> <ul> <li>First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.</li> <li>Secondly, the value of the parent node should be greater than the either of its child.</li> </ul> <p> <strong>Step 1:</strong> First we add the 44 element in the tree as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-5.webp" alt="Heap Data Structure"> <p> <strong>Step 2:</strong> The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-6.webp" alt="Heap Data Structure"> <p> <strong>Step 3:</strong> The next element is 77 and it will be added to the right of the 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-7.webp" alt="Heap Data Structure"> <p>As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-8.webp" alt="Heap Data Structure"> <p> <strong>Step 4:</strong> The next element is 11. The node 11 is added to the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-9.webp" alt="Heap Data Structure"> <p> <strong>Step 5:</strong> The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-10.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below:< p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-11.webp" alt="Heap Data Structure"> <p> <strong>Step 6:</strong> The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-12.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:< p> <p>Again, it is violating the max heap property because 88>77 so we will swap these two values as shown below:</p> <p> <strong>Step 7:</strong> The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:</p> <p>In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.</p> <p> <strong>Deletion in Heap Tree</strong> </p> <p>In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.</p> <p> <strong>Let's understand the deletion through an example.</strong> </p> <p> <strong>Step 1</strong> : In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:</p> <p>Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:</p> <p>Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.</p> <p> <strong>Algorithm to heapify the tree</strong> </p> <pre> MaxHeapify(A, n, i) { int largest =i; int l= 2i; int r= 2i+1; while(lA[largest]) { largest=l; } while(rA[largest]) { largest=r; } if(largest!=i) { swap(A[largest], A[i]); heapify(A, n, largest); }} </pre> <hr></88,></p></55,></p></a[i])> 