Prvo ćemo razumjeti binarno stablo i binarno stablo pretraživanja odvojeno, a zatim ćemo pogledati razlike između binarnog stabla i binarnog stabla pretraživanja.

Što je binarno stablo?

A Binarno stablo jePokazivač na lijevo dijete:Pohranjuje referencu lijevog podređenog čvora.Pokazivač na pravo dijete:Pohranjuje referencu desnog podređenog čvora.Element podataka:Element podataka je vrijednost podataka koju pohranjuje čvor.

Binarno stablo se može predstaviti kao:

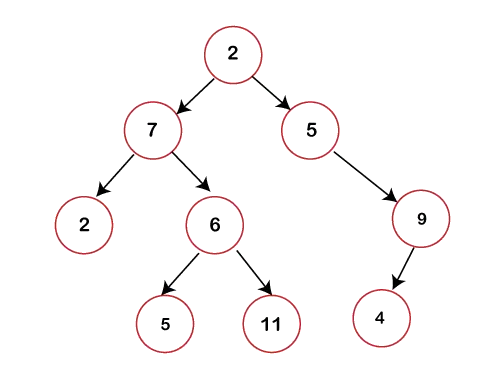
Na gornjoj slici možemo vidjeti da svaki čvor sadrži najviše 2 djeteta. Ako bilo koji čvor ne sadrži lijevo ili desno dijete tada bi vrijednost pokazivača s obzirom na to dijete bila NULL.

Osnovna terminologija koja se koristi u binarnom stablu je:

Korijenski čvor:Korijenski čvor je prvi ili najviši čvor u binarnom stablu.Nadređeni čvor:Kada je čvor povezan s drugim čvorom kroz rubove, tada je taj čvor poznat kao nadređeni čvor. U binarnom stablu roditeljski čvor može imati najviše 2 djece.Podređeni čvor:Ako čvor ima svog prethodnika, tada je taj čvor poznat kao a dijete čvor .Listni čvor:Čvor koji ne sadrži dijete poznat kao a lisni čvor .Interni čvor:Čvor koji ima najmanje 2 djece poznat kao an unutarnji čvor .Dubina čvora:Udaljenost od korijenskog čvora do danog čvora poznata je kao a dubina čvora . Dajemo oznake svim čvorovima kao što je korijenski čvor označen s 0 jer nema dubinu, djeca korijenskih čvorova označena su s 1, djeca korijenskog djeteta označena su s 2.Visina:Najveća udaljenost od korijenskog čvora do lisnog čvora je visina čvora .

U binarnom stablu postoji jedno stablo poznato kao a savršeno binarno stablo . To je stablo u kojem svi unutarnji čvorovi moraju sadržavati dva čvora, a svi lisnati čvorovi moraju biti na istoj dubini. U slučaju savršenog binarnog stabla, ukupan broj čvorova koji postoje u binarnom stablu može se izračunati pomoću sljedeće jednadžbe:

n = 2^m+1-1

gdje je n broj čvorova, m je dubina čvora.

Što je stablo binarnog pretraživanja?

A Binarno stablo pretraživanja je stablo koje slijedi određeni redoslijed rasporeda elemenata, dok binarno stablo ne slijedi nikakav redoslijed. U stablu binarnog pretraživanja, vrijednost lijevog čvora mora biti manja od nadređenog čvora, a vrijednost desnog čvora mora biti veća od nadređenog čvora.

Razumimo koncept binarnog stabla pretraživanja kroz primjere.

Na gornjoj slici možemo vidjeti da je vrijednost korijenskog čvora 15, što je veće od vrijednosti svih čvorova u lijevom podstablu. Vrijednost korijenskog čvora manja je od vrijednosti svih čvorova u desnom podstablu. Sada prelazimo na lijevo dijete korijenskog čvora. 10 je veće od 8 i manje od 12; također zadovoljava svojstvo binarnog stabla pretraživanja. Sada prelazimo na desno dijete korijenskog čvora; vrijednost 20 je veća od 17 i manja od 25; također zadovoljava svojstvo binarnog stabla pretraživanja. Stoga možemo reći da je gore prikazano stablo binarno stablo pretraživanja.

Sada, ako promijenimo vrijednost 12 u 16 u gornjem binarnom stablu, moramo saznati je li to još uvijek binarno stablo pretraživanja ili ne.

Vrijednost korijenskog čvora je 15 što je veće od 10, ali manje od 16, tako da ne zadovoljava svojstvo stabla binarnog pretraživanja. Stoga, to nije binarno stablo pretraživanja.

Operacije na stablu binarnog pretraživanja

Možemo izvoditi operacije umetanja, brisanja i pretraživanja na stablu binarnog pretraživanja. Hajdemo razumjeti kako se pretraživanje izvodi na binarnom pretraživanju. Dolje je prikazano binarno stablo na kojem moramo izvršiti operaciju pretraživanja:

Pretpostavimo da moramo pretražiti 10 u gornjem binarnom stablu. Da bismo izvršili binarno pretraživanje, razmotrit ćemo sve cijele brojeve u sortiranom nizu. Prvo stvaramo potpuni popis u prostoru za pretraživanje i svi će brojevi postojati u prostoru za pretraživanje. Prostor za pretraživanje označen je s dva pokazivača, tj. početkom i krajem. Niz gornjeg binarnog stabla može se predstaviti kao

Prvo ćemo izračunati srednji element i usporediti srednji element s elementom koji treba pretraživati. Srednji element izračunava se pomoću n/2. Vrijednost n je 7; dakle, srednji element je 15. Srednji element nije jednak traženom elementu, tj. 10.

Napomena: Ako je element koji se traži manji od srednjeg elementa, tada će se pretraživanje izvršiti u lijevoj polovici; inače će se pretraživanje vršiti na desnoj polovici. U slučaju jednakosti, element je pronađen.

Budući da je element koji se traži manji od srednjeg elementa, pretraživanje će se izvršiti na lijevom nizu. Sada je pretraga smanjena na pola, kao što je prikazano u nastavku:

Srednji element u lijevom nizu je 10, što je jednako traženom elementu.

Vremenska složenost

U binarnom pretraživanju postoji n elemenata. Ako srednji element nije jednak traženom elementu, tada se prostor pretraživanja smanjuje na n/2, a mi ćemo nastaviti smanjivati ​​prostor pretraživanja za n/2 dok ne pronađemo element. U cijeloj redukciji, ako se pomaknemo od n do n/2 do n/4 i tako dalje, tada će trebati log₂n koraka.

Razlike između binarnog stabla i binarnog stabla pretraživanja