Bellman ford algoritam je algoritam najkraćeg puta s jednim izvorom. Ovaj se algoritam koristi za pronalaženje najkraće udaljenosti od jednog vrha do svih ostalih vrhova ponderiranog grafa. Postoje razni drugi algoritmi koji se koriste za pronalaženje najkraćeg puta poput Dijkstra algoritma, itd. Ako ponderirani graf sadrži negativne vrijednosti težine, tada Dijkstra algoritam ne potvrđuje daje li točan odgovor ili ne. Za razliku od Dijkstra algoritma, bellman ford algoritam jamči točan odgovor čak i ako težinski graf sadrži negativne vrijednosti težine.
Pravilo ovog algoritma
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Razmotrite donji grafikon:
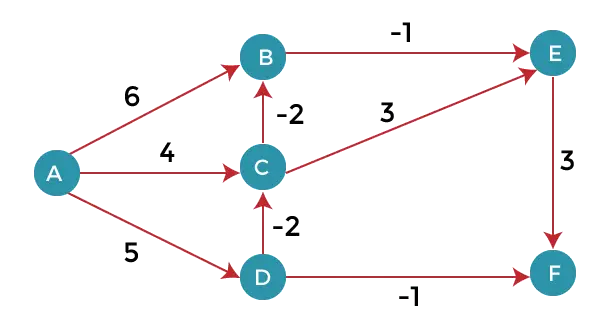
Kao što možemo primijetiti na gornjem grafikonu, neki od pondera su negativni. Gornji graf sadrži 6 vrhova tako da ćemo se opustiti do 5 vrhova. Ovdje ćemo opustiti sve rubove 5 puta. Petlja će se ponoviti 5 puta kako bi se dobio točan odgovor. Ako se petlja ponavlja više od 5 puta, tada će i odgovor biti isti, tj. neće biti promjene u udaljenosti između vrhova.
Opuštanje znači:
popis fontova u gimp-u
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
Dakle, udaljenost vrha B je 6.
Razmotrite rub (A, C). Označite vrh 'A' kao 'u', a vrh 'C' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 0
d(v) = ∞
c(u , v) = 4
Budući da je (0 + 4) manje od ∞, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Dakle, udaljenost vrha C je 4.
Razmotrite rub (A, D). Označite vrh 'A' kao 'u', a vrh 'D' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 0
d(v) = ∞
c(u, v) = 5
Budući da je (0 + 5) manje od ∞, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
Dakle, udaljenost vrha D je 5.
Razmotrite rub (B, E). Označite vrh 'B' kao 'u', a vrh 'E' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 6
d(v) = ∞
c(u , v) = -1
Budući da je (6 - 1) manje od ∞, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 6 - 1 = 5
Dakle, udaljenost vrha E je 5.
Razmotrite rub (C, E). Označite vrh 'C' kao 'u', a vrh 'E' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 4
d(v) = 5
c(u , v) = 3
Budući da je (4 + 3) veće od 5, neće biti ažuriranja. Vrijednost u vrhu E je 5.
Razmotrite rub (D, C). Označite vrh 'D' kao 'u', a vrh 'C' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 5
d(v) = 4
c(u , v) = -2
Budući da je (5 -2) manje od 4, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
java provjera je nula
Dakle, udaljenost vrha C je 3.
Razmotrite rub (D, F). Označite vrh 'D' kao 'u', a vrh 'F' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 5
d(v) = ∞
c(u , v) = -1
Budući da je (5 -1) manje od ∞, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
Dakle, udaljenost vrha F je 4.
Razmotrite rub (E, F). Označite vrh 'E' kao 'u', a vrh 'F' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 5
d(v) = ∞
c(u , v) = 3
Budući da je (5 + 3) veće od 4, ne bi bilo ažuriranja vrijednosti udaljenosti vrha F.
Razmotrite rub (C, B). Označite vrh 'C' kao 'u', a vrh 'B' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 3
d(v) = 6
c(u , v) = -2
Budući da je (3 - 2) manje od 6, ažurirajte
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
Dakle, udaljenost vrha B je 1.
Sada je prva iteracija dovršena. Prelazimo na drugu iteraciju.
Druga iteracija:
U drugoj iteraciji ponovno provjeravamo sve rubove. Prvi rub je (A, B). Budući da je (0 + 6) veće od 1, ne bi bilo ažuriranja u vrhu B.
Sljedeći rub je (A, C). Budući da je (0 + 4) veće od 3, ne bi bilo ažuriranja u vrhu C.
Sljedeći rub je (A, D). Budući da je (0 + 5) jednako 5, ne bi bilo ažuriranja u vrhu D.
Sljedeći rub je (B, E). Budući da je (1 - 1) jednako 0 što je manje od 5, ažurirajte:
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B , E)
= 1 - 1 = 0
Sljedeći rub je (C, E). Budući da je (3 + 3) jednako 6 što je veće od 5, ne bi bilo ažuriranja u vrhu E.
Sljedeći rub je (D, C). Budući da je (5 - 2) jednako 3, ne bi bilo ažuriranja u vrhu C.
Sljedeći rub je (D, F). Budući da je (5 - 1) jednako 4, ne bi bilo ažuriranja u vrhu F.
Sljedeći rub je (E, F). Budući da je (5 + 3) jednako 8 što je veće od 4, ne bi bilo ažuriranja u vrhu F.
Sljedeći rub je (C, B). Budući da je (3 - 2) jednako 1`, ne bi bilo ažuriranja u vrhu B.

Treća iteracija
Provest ćemo iste korake kao u prethodnim iteracijama. Primijetit ćemo da neće biti ažuriranja u udaljenosti vrhova.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Vremenska složenost
Vremenska složenost Bellman ford algoritma bila bi O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
Dakle, udaljenost vrha 3 je 5.
Razmotrite rub (1, 2). Označite vrh '1' kao 'u', a vrh '2' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 0
d(v) = ∞
c(u , v) = 4
Budući da je (0 + 4) manje od ∞, ažuriraj
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Dakle, udaljenost vrha 2 je 4.
Razmotrite rub (3, 2). Označite vrh '3' kao 'u', a vrh '2' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 5
d(v) = 4
c(u , v) = 7
Budući da je (5 + 7) veće od 4, ne bi bilo ažuriranja u vrhu 2.
Razmotrite rub (2, 4). Označite vrh '2' kao 'u', a vrh '4' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 4
d(v) = ∞
c(u , v) = 7
Budući da je (4 + 7) jednako 11 što je manje od ∞, ažurirajte
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
for petlja u Javi
Dakle, udaljenost vrha 4 je 11.
Razmotrite rub (4, 3). Označite vrh '4' kao 'u', a vrh '3' kao 'v'. Sada upotrijebite opuštajuću formulu:
d(u) = 11
d(v) = 5
c(u, v) = -15
Budući da je (11 - 15) jednako -4 što je manje od 5, ažurirajte
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
Dakle, udaljenost vrha 3 je -4.
Sada prelazimo na drugu iteraciju.
Druga iteracija
Sada ćemo ponovno provjeriti sve rubove. Prvi rub je (1, 3). Budući da je (0 + 5) jednako 5 što je veće od -4, tako da ne bi bilo ažuriranja u vrhu 3.
Sljedeći rub je (1, 2). Budući da je (0 + 4) jednako 4, ne bi bilo ažuriranja u vrhu 2.
Sljedeći rub je (3, 2). Budući da je (-4 + 7) jednako 3 što je manje od 4, ažurirajte:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Stoga je vrijednost u vrhu 2 3.
Sljedeći rub je (2, 4). Budući da je ( 3+7) jednako 10 što je manje od 11, ažurirajte
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Stoga je vrijednost u vrhu 4 10.
java karta
Sljedeći rub je (4, 3). Budući da je (10 - 15) jednako -5 što je manje od -4, ažurirajte:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Stoga je vrijednost u vrhu 3 -5.
Sada prelazimo na treću iteraciju.
Treća iteracija
Sada ćemo ponovno provjeriti sve rubove. Prvi rub je (1, 3). Budući da je (0 + 5) jednako 5 što je veće od -5, tako da ne bi bilo ažuriranja u vrhu 3.
Sljedeći rub je (1, 2). Budući da je (0 + 4) jednako 4 što je veće od 3, tako da ne bi bilo ažuriranja u vrhu 2.
Sljedeći rub je (3, 2). Budući da je (-5 + 7) jednako 2 što je manje od 3, ažurirajte:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Stoga je vrijednost u vrhu 2 2.
Sljedeći rub je (2, 4). Budući da je (2 + 7) jednako 9 što je manje od 10, ažurirajte:
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Stoga je vrijednost u vrhu 4 9.
Sljedeći rub je (4, 3). Budući da je (9 - 15) jednako -6 što je manje od -5, ažurirajte:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Stoga je vrijednost u vrhu 3 -6.

Budući da graf sadrži 4 vrha, prema bellman ford algoritmu, bile bi samo 3 iteracije. Ako pokušamo izvesti 4thiteracije na grafu, udaljenost vrhova od zadanog vrha ne bi se trebala mijenjati. Ako udaljenost varira, to znači da bellman ford algoritam ne daje točan odgovor.
4thponavljanje
Prvi rub je (1, 3). Budući da je (0 +5) jednako 5 što je veće od -6, tako da ne bi bilo promjene u vrhu 3.
Sljedeći rub je (1, 2). Budući da je (0 + 4) veće od 2, ne bi bilo ažuriranja.
Sljedeći rub je (3, 2). Budući da je (-6 + 7) jednako 1 što je manje od 3, ažurirajte:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
U ovom slučaju, vrijednost vrha se ažurira. Dakle, zaključujemo da bellman ford algoritam ne radi kada graf sadrži ciklus negativne težine.
Stoga je vrijednost u vrhu 2 1.
