Stog je linearna struktura podataka koja slijedi LIFO (posljednji ušao prvi izašao) načelo. Stog ima jedan kraj, dok red čekanja ima dva kraja ( sprijeda i straga ). Sadrži samo jedan pokazivač gornji pokazivač pokazujući na najviši element hrpe. Kad god se element doda u stog, dodaje se na vrh stoga, a element se može izbrisati samo sa stoga. Drugim riječima, a stog se može definirati kao spremnik u kojem se umetanje i brisanje može učiniti s jednog kraja poznatog kao vrh stoga.

Neke ključne točke vezane uz stog

• Naziva se hrpom jer se ponaša kao stog iz stvarnog svijeta, hrpe knjiga itd.
• Stog je apstraktni tip podataka s unaprijed definiranim kapacitetom, što znači da može pohraniti elemente ograničene veličine.
• To je struktura podataka koja slijedi neki redoslijed za umetanje i brisanje elemenata, a taj redoslijed može biti LIFO ili FILO.

Rad snopa

Stack radi na LIFO uzorku. Kao što možemo vidjeti na donjoj slici, postoji pet memorijskih blokova u stogu; stoga je veličina hrpe 5.

proljetna čizma

Pretpostavimo da želimo pohraniti elemente u stog i pretpostavimo da je taj stog prazan. Uzeli smo hrpu veličine 5 kao što je prikazano dolje u kojoj guramo elemente jedan po jedan dok se hrpa ne napuni.

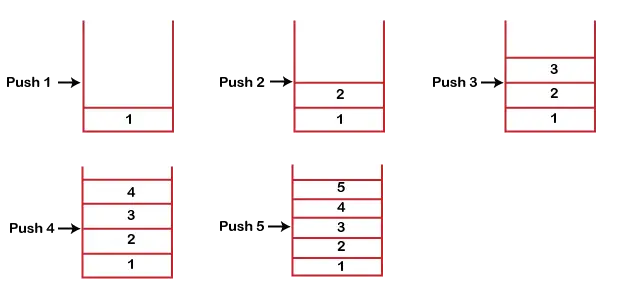
Budući da je naš stog pun jer je veličina stoga 5. U gornjim slučajevima možemo primijetiti da ide od vrha prema dnu kada smo unosili novi element u stog. Hrpa se puni od dna prema vrhu.

Kada izvodimo operaciju brisanja na stogu, postoji samo jedan način za ulaz i izlaz jer je drugi kraj zatvoren. Slijedi obrazac LIFO, što znači da će vrijednost koja je prva unesena biti zadnja uklonjena. U gornjem slučaju prvo se upisuje vrijednost 5, pa će ona biti uklonjena tek nakon brisanja svih ostalih elemenata.

Standardne operacije snopa

Slijede neke uobičajene operacije implementirane na stogu:

gurnuti():Kada umetnemo element u stog, tada je operacija poznata kao guranje. Ako je stog pun tada dolazi do stanja preljeva.pop():Kada izbrišemo element sa steka, operacija je poznata kao pop. Ako je stog prazan znači da nijedan element ne postoji u stogu, to je stanje poznato kao stanje podnošenja.prazno je():Određuje je li stog prazan ili ne.puno je():Određuje je li stog pun ili ne.'zaviriti():Vraća element na zadanu poziciju.računati():Vraća ukupan broj elemenata dostupnih u nizu.promijeniti():Mijenja element na zadanoj poziciji.prikaz():Ispisuje sve elemente dostupne u nizu.

PUSH operacija

Koraci uključeni u operaciju PUSH navedeni su u nastavku:

linux kako preimenovati direktorij

• Prije umetanja elementa u stog, provjeravamo da li je stog pun.
• Ako pokušamo umetnuti element u stog, a stog je pun, tada je prelijevanje javlja se stanje.
• Kada inicijaliziramo stog, postavljamo vrijednost vrha na -1 da provjerimo je li stog prazan.
• Kada se novi element gurne u stog, prvo se povećava vrijednost vrha, tj. vrh=vrh+1, i element će biti postavljen na novu poziciju vrh .
• Elementi će se umetati dok ne dođemo do max veličina hrpe.

POP operacija

Koraci uključeni u POP operaciju navedeni su u nastavku:

• Prije brisanja elementa sa steka provjeravamo da li je stog prazan.
• Ako pokušamo izbrisati element iz praznog stoga, tada se donji tok javlja se stanje.
• Ako stog nije prazan, prvo pristupamo elementu na koji pokazuje vrh
• Nakon što se izvede operacija iskakanja, vrh se smanjuje za 1, tj. vrh=top-1 .

Primjene Stacka

Sljedeće su primjene hrpe:

Balansiranje simbola:Stog se koristi za balansiranje simbola. Na primjer, imamo sljedeći program:

 int main() { cout&lt;<'hello'; cout<<'javatpoint'; } < pre> <p>As we know, each program has <em>an opening</em> and <em>closing</em> braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.</p> <ul> <tr><td>String reversal:</td> Stack is also used for reversing a string. For example, we want to reverse a &apos; <strong>javaTpoint</strong> &apos; string, so we can achieve this with the help of a stack. <br> First, we push all the characters of the string in a stack until we reach the null character. <br> After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack. </tr><tr><td>UNDO/REDO:</td> It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write &apos;a&apos;, then &apos;b&apos;, and then &apos;c&apos;; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state. <br> If we want to perform UNDO operation, and want to achieve &apos;ab&apos; state, then we implement pop operation. </tr><tr><td>Recursion:</td> The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained. </tr><tr><td>DFS(Depth First Search):</td> This search is implemented on a Graph, and Graph uses the stack data structure. </tr><tr><td>Backtracking:</td> Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure. </tr><tr><td>Expression conversion:</td> Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below: <pre>Infix to prefix Infix to postfix Prefix to infix Prefix to postfix Postfix to infix</pre> </tr><tr><td>Memory management:</td> The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released. </tr></ul> <hr></'hello';>