• Naivni Bayesov algoritam je algoritam nadziranog učenja koji se temelji na Bayesov teorem i koristi se za rješavanje problema klasifikacije.
• Uglavnom se koristi u klasifikacija teksta koji uključuje visokodimenzionalni skup podataka za obuku.
• Naivni Bayesov klasifikator jedan je od jednostavnih i najučinkovitijih algoritama za klasifikaciju koji pomaže u izgradnji brzih modela strojnog učenja koji mogu napraviti brza predviđanja.
To je probabilistički klasifikator, što znači da predviđa na temelju vjerojatnosti objekta.
• Neki popularni primjeri Naivnog Bayesovog algoritma su filtriranje spama, sentimentalna analiza i klasificiranje članaka .

Zašto se zove Naivni Bayes?

Algoritam Naive Bayes sastoji se od dvije riječi Naive i Bayes, koje se mogu opisati kao:

Naivan: Naziva se naivnim jer pretpostavlja da je pojava određene značajke neovisna o pojavi drugih značajki. Na primjer, ako se voće identificira na temelju boje, oblika i okusa, tada se crveno, sferično i slatko voće prepoznaje kao jabuka. Stoga svaka značajka zasebno pridonosi prepoznavanju da se radi o jabuci bez ovisnosti jedna o drugoj.Bayes: Zove se Bayes jer ovisi o načelu Bayesovog teorema.

Bayesov teorem:

• Bayesov teorem je također poznat kao Bayesovo pravilo ili Bayesov zakon , koji se koristi za određivanje vjerojatnosti hipoteze s prethodnim znanjem. Ovisi o uvjetnoj vjerojatnosti.
• Formula za Bayesov teorem dana je kao:

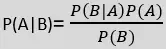
Gdje,

P(A|B) je posteriorna vjerojatnost : Vjerojatnost hipoteze A o promatranom događaju B.

P(B|A) je vjerojatnost vjerojatnosti : Vjerojatnost dokaza s obzirom da je vjerojatnost hipoteze istinita.

P(A) je prethodna vjerojatnost : Vjerojatnost hipoteze prije promatranja dokaza.

instanceof

P(B) je granična vjerojatnost : Vjerojatnost dokaza.

Rad Naivnog Bayesovog klasifikatora:

Rad naivnog Bayesovog klasifikatora može se razumjeti uz pomoć donjeg primjera:

Pretpostavimo da imamo skup podataka od vremenski uvjeti i odgovarajuća ciljna varijabla ' igra '. Dakle, pomoću ovog skupa podataka moramo odlučiti hoćemo li igrati ili ne na određeni dan u skladu s vremenskim uvjetima. Da bismo riješili ovaj problem, moramo slijediti korake u nastavku:

1. Pretvorite dani skup podataka u tablice frekvencija.
2. Generirajte tablicu vjerojatnosti pronalaženjem vjerojatnosti zadanih značajki.
3. Sada upotrijebite Bayesov teorem za izračunavanje posteriorne vjerojatnosti.

Problem : Ako je vrijeme sunčano, onda bi igrač trebao igrati ili ne?

Riješenje : Da biste to riješili, prvo razmotrite skup podataka u nastavku:

Tablica učestalosti za vremenske uvjete:

Vremenski uvjeti tablice vjerojatnosti:

Primjena Bayesovog teorema:

P(Da|Sunčano)= P(Sunčano|Da)*P(Da)/P(Sunčano)

P(Sunčano|Da)= 3/10= 0,3

P(sunčano)= 0,35

P(Da)=0,71

10 ml u oz

Dakle, P(Da|Sunčano) = 0,3*0,71/0,35= 0,60

P(Ne|Sunčano)= P(Sunčano|Ne)*P(Ne)/P(Sunčano)

P(Sunčano|NE)= 2/4=0,5

P(ne)= 0,29

P(sunčano)= 0,35

Dakle, P(Ne|Sunčano)= 0,5*0,29/0,35 = 0,41

Dakle, kao što možemo vidjeti iz gornjeg izračuna da P(Da|Sunčano)>P(Ne|Sunčano)

Stoga na sunčanom danu igrač može igrati igru.

Prednosti Naivnog Bayesovog klasifikatora:

• Naivni Bayes jedan je od brzih i jednostavnih ML algoritama za predviđanje klase skupova podataka.
• Može se koristiti za binarne kao i za višeklasne klasifikacije.
• U usporedbi s drugim algoritmima dobro radi u predviđanjima više klasa.
• To je najpopularniji izbor za problemi klasifikacije teksta .

Nedostaci Naivnog Bayesovog klasifikatora:

• Naivni Bayes pretpostavlja da su sve značajke neovisne ili nepovezane, tako da ne može naučiti odnos između značajki.

Primjene Naivnog Bayesovog klasifikatora:

• Koristi se za Kreditno bodovanje .
• Koristi se u klasifikacija medicinskih podataka .
• Može se koristiti u predviđanja u stvarnom vremenu jer naivni Bayesov klasifikator revno uči.
• Koristi se u klasifikaciji teksta kao što je Filtriranje neželjene pošte i Analiza sentimenta .

Vrste naivnog Bayesovog modela:

Postoje tri vrste naivnog Bayesovog modela, koji su navedeni u nastavku:

Gaussov: Gaussov model pretpostavlja da značajke slijede normalnu distribuciju. To znači da ako prediktori uzimaju kontinuirane vrijednosti umjesto diskretnih, tada model pretpostavlja da su te vrijednosti uzorkovane iz Gaussove distribucije.Multinom: multinomski naivni Bayesov klasifikator koristi se kada su podaci multinomijalno distribuirani. Prvenstveno se koristi za probleme klasifikacije dokumenata, znači da određeni dokument pripada kojoj kategoriji kao što su sport, politika, obrazovanje itd.
Klasifikator koristi učestalost riječi za prediktore.Bernoulli: Bernoullijev klasifikator radi slično multinomskom klasifikatoru, ali prediktorske varijable su nezavisne Booleove varijable. Na primjer postoji li određena riječ u dokumentu ili ne. Ovaj je model također poznat po zadacima klasifikacije dokumenata.

Python implementacija algoritma Naive Bayes:

Sada ćemo implementirati naivni Bayesov algoritam koristeći Python. Dakle, za ovo ćemo koristiti ' korisnički podaci ' skup podataka , koji smo koristili u našem drugom modelu klasifikacije. Stoga možemo lako usporediti Naive Bayesov model s ostalim modelima.

Koraci za implementaciju:

• Korak prethodne obrade podataka
• Uklapanje Naive Bayesa u set za obuku
• Predviđanje rezultata testa
• Testirajte točnost rezultata (Stvaranje matrice zabune)
• Vizualizacija rezultata ispitnog skupa.

1) Korak prethodne obrade podataka:

U ovom koraku unaprijed ćemo obraditi/pripremiti podatke kako bismo ih mogli učinkovito koristiti u našem kodu. Slično je kao što smo radili u prethodnoj obradi podataka. Kôd za ovo naveden je u nastavku:

 Importing the libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd # Importing the dataset dataset = pd.read_csv('user_data.csv') x = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values # Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0) # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() x_train = sc.fit_transform(x_train) x_test = sc.transform(x_test) 

U gornjem kodu, učitali smo skup podataka u naš program koristeći ' skup podataka = pd.read_csv('user_data.csv') . Učitani skup podataka podijeljen je na set za obuku i skup za testiranje, a zatim smo skalirali varijablu značajke.

avl stabla

Izlaz za skup podataka dan je kao:

2) Uklapanje Naive Bayesa u set za vježbanje:

Nakon koraka predobrade, sada ćemo uklopiti Naive Bayesov model u set za obuku. Ispod je kod za to:

 # Fitting Naive Bayes to the Training set from sklearn.naive_bayes import GaussianNB classifier = GaussianNB() classifier.fit(x_train, y_train) 

U gornjem kodu koristili smo Gaussov NB klasifikator kako bi ga prilagodili skupu podataka za obuku. Također možemo koristiti druge klasifikatore prema našim zahtjevima.

Izlaz:

 Out[6]: GaussianNB(priors=None, var_smoothing=1e-09) 

3) Predviđanje rezultata skupa testova:

Sada ćemo predvidjeti rezultat skupa testova. Za to ćemo stvoriti novu varijablu prediktora y_pred , te će koristiti funkciju predviđanja za izradu predviđanja.

 # Predicting the Test set results y_pred = classifier.predict(x_test) 

Izlaz:

Gornji izlaz prikazuje rezultat za vektor predviđanja y_pred i realni vektor y_test. Možemo vidjeti da se neka predviđanja razlikuju od stvarnih vrijednosti, što su netočna predviđanja.

4) Stvaranje matrice zabune:

Sada ćemo provjeriti točnost Naive Bayesovog klasifikatora pomoću matrice zabune. Ispod je kod za to:

 # Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) 

Izlaz:

Kao što možemo vidjeti u gornjem rezultatu matrice zabune, postoji 7+3= 10 netočnih predviđanja i 65+25=90 točnih predviđanja.

mvc u proljetnom okviru

5) Vizualizacija rezultata skupa treninga:

Zatim ćemo vizualizirati rezultat skupa za obuku koristeći Na�ve Bayesov klasifikator. Ispod je kod za to:

 # Visualising the Training set results from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Izlaz:

U gornjem izlazu možemo vidjeti da je Na�ve Bayesov klasifikator razdvojio podatkovne točke finom granicom. To je Gaussova krivulja kakvu smo koristili GaussovNB klasifikator u našem kodu.

6) Vizualizacija rezultata testa:

 # Visualising the Test set results from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Izlaz:

Gornji izlaz je konačni izlaz za podatke skupa testova. Kao što vidimo, klasifikator je stvorio Gaussovu krivulju da podijeli varijable 'kupljeno' i 'nekupljeno'. Postoje neka pogrešna predviđanja koja smo izračunali u matrici zabune. Ali ipak je prilično dobar klasifikator.