Linearna regresija i logistička regresija dva su poznata algoritma strojnog učenja koji spadaju u tehniku nadziranog učenja. Budući da su oba algoritma nadzirane prirode, ovi algoritmi koriste označeni skup podataka za izradu predviđanja. Ali glavna razlika između njih je način na koji se koriste. Linearna regresija se koristi za rješavanje problema regresije, dok se logistička regresija koristi za rješavanje problema klasifikacije. Opis oba algoritma dan je u nastavku zajedno s tablicom razlika.
Linearna regresija:
- Linearna regresija jedan je od najjednostavnijih algoritama strojnog učenja koji spada u tehniku nadziranog učenja i koristi se za rješavanje problema regresije.
- Koristi se za predviđanje kontinuirane zavisne varijable uz pomoć nezavisnih varijabli.
- Cilj linearne regresije je pronaći liniju koja najbolje odgovara koja može točno predvidjeti izlaz za kontinuiranu zavisnu varijablu.
- Ako se za predviđanje koristi jedna nezavisna varijabla, to se naziva jednostavna linearna regresija, a ako postoji više od dvije neovisne varijable, takva se regresija naziva višestruka linearna regresija.
- Pronalaženjem linije koja najbolje odgovara, algoritam uspostavlja odnos između zavisne varijable i nezavisne varijable. I odnos bi trebao biti linearne prirode.
- Izlaz za linearnu regresiju trebaju biti samo kontinuirane vrijednosti kao što su cijena, dob, plaća itd. Odnos između zavisne varijable i nezavisne varijable može se prikazati na slici ispod:

Na gornjoj slici zavisna varijabla je na Y-osi (plaća), a nezavisna varijabla na x-osi (iskustvo). Regresijska linija se može napisati kao:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Gdje0i a1su koeficijenti, a ε je izraz pogreške.
Logistička regresija:
- Logistička regresija jedan je od najpopularnijih algoritama strojnog učenja koji spada u tehnike nadziranog učenja.
- Može se koristiti za probleme klasifikacije kao i za probleme regresije, ali se uglavnom koristi za probleme klasifikacije.
- Logistička regresija koristi se za predviđanje kategoričke zavisne varijable uz pomoć nezavisnih varijabli.
- Izlaz problema logističke regresije može biti samo između 0 i 1.
- Logistička regresija se može koristiti tamo gdje su potrebne vjerojatnosti između dvije klase. Na primjer hoće li danas padati kiša ili ne, 0 ili 1, točno ili netočno itd.
- Logistička regresija temelji se na konceptu procjene maksimalne vjerojatnosti. Prema ovoj procjeni, promatrani podaci trebali bi biti najvjerojatniji.
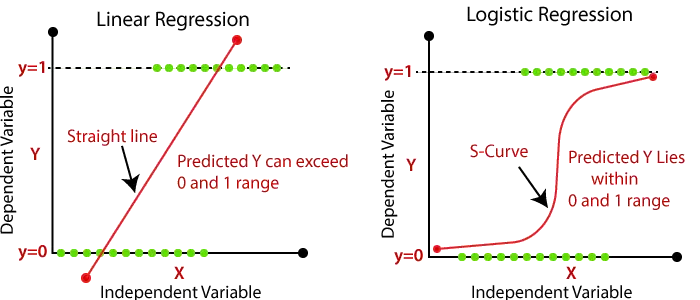
- U logističkoj regresiji, ponderirani zbroj inputa prolazimo kroz aktivacijsku funkciju koja može mapirati vrijednosti između 0 i 1. Takva aktivacijska funkcija poznata je kao sigmoidna funkcija a dobivena krivulja naziva se sigmoidna krivulja ili S-krivulja. Razmotrite sliku u nastavku:

- Jednadžba za logističku regresiju je:

Razlika između linearne regresije i logističke regresije:
| Linearna regresija | Logistička regresija |
|---|---|
| Linearna regresija koristi se za predviđanje kontinuirane ovisne varijable pomoću danog skupa nezavisnih varijabli. | Logistička regresija koristi se za predviđanje kategoričke zavisne varijable pomoću zadanog skupa nezavisnih varijabli. |
| Linearna regresija se koristi za rješavanje problema regresije. | Logistička regresija se koristi za rješavanje problema klasifikacije. |
| U linearnoj regresiji predviđamo vrijednost kontinuiranih varijabli. | U logističkoj regresiji predviđamo vrijednosti kategoričkih varijabli. |
| U linearnoj regresiji pronalazimo liniju koja najbolje odgovara, pomoću koje možemo lako predvidjeti izlaz. | U logističkoj regresiji nalazimo S-krivulju prema kojoj možemo klasificirati uzorke. |
| Za procjenu točnosti koristi se metoda najmanjeg kvadrata. | Za procjenu točnosti koristi se metoda procjene najveće vjerojatnosti. |
| Izlaz za linearnu regresiju mora biti kontinuirana vrijednost, poput cijene, starosti itd. | Izlaz logističke regresije mora biti kategorička vrijednost kao što je 0 ili 1, Da ili Ne, itd. |
| U linearnoj regresiji zahtijeva se da odnos između zavisne varijable i nezavisne varijable mora biti linearan. | U logističkoj regresiji nije potreban linearni odnos između zavisne i nezavisne varijable. |
| U linearnoj regresiji može postojati kolinearnost između nezavisnih varijabli. | U logističkoj regresiji ne bi trebalo postojati kolinearnost između nezavisne varijable. |
