U Javi, Heap je posebna vrsta strukture podataka gdje se korijenski čvor ili nadređeni čvor uspoređuje sa svojim lijevim i desnim potomcima i raspoređuje prema redoslijedu. Pretpostavimo da je x korijenski čvor, a y dijete čvor, svojstvo tipka (x)<= key(y)< strong>će generirati min-heap, a ta relacija se naziva 'Svojstvo gomile' .
Na temelju redoslijeda nadređenih i podređenih čvorova, Heap se može klasificirati u dva oblika, tj. Min heap i Max heap. Razmotrimo oba, jednog po jednog i implementirajmo kod u Javi.
Min hrpa
Min heap je posebna vrsta strukture podataka hrpe koja je sama po sebi potpuno binarno stablo. Min heap ima sljedeća svojstva:
- Vrijednost korijenskog čvora uvijek je manja u usporedbi s drugim čvorovima hrpe.
- Svaki interni čvor ima ključnu vrijednost koja je uvijek manja ili jednaka svojoj djeci.
Možemo izvesti sljedeće tri operacije u Min heapu:
umetničvor()
Možemo izvesti umetanje u Min hrpu dodavanjem novog ključa na kraju stabla. Ako je vrijednost umetnutog ključa manja od njegovog nadređenog čvora, moramo preći ključ prema gore da bismo ispunili svojstvo hrpe. Proces umetanja traje O(log n) vremena.
ekstraktMin()
To je jedna od najvažnijih operacija koje izvodimo za uklanjanje čvora minimalne vrijednosti, tj. korijenskog čvora gomile. Nakon uklanjanja korijenskog čvora, moramo biti sigurni da se svojstvo hrpe treba održavati. Operaciji extractMin() potrebno je O(Logn) vremena za uklanjanje minimalnog elementa iz hrpe.
getMin()
The getMin() operacija se koristi za dobivanje korijenskog čvora gomile, tj. minimalnog elementa u O(1) vremenu.
Primjer:
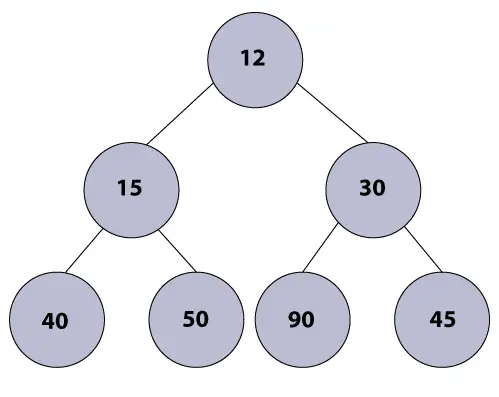
Min algoritam gomile
proceduredesign_min_heap Array arr: of size n => array of elements // call min_heapify procedure for each element of the array to form min heap repeat for (k = n/2 ; k >= 1 ; k--) call procedure min_heapify (arr, k); proceduremin_heapify (vararr[ ] , var k, varn) { varleft_child = 2*k; varright_child = 2*k+1; var smallest; if(left_child<= n and arr[left_child ] <arr[ k ) smallest="left_child;" else if(right_child<="n" arr[right_child <arr[smallest] if(smallest !="k)" { swaparr[ arr[ ]); callmin_heapify (arr, smallest, n); } < pre> <p> <strong>MinHeapJavaImplementation.java</strong> </p> <pre> // import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; // create class MinHeap to construct Min heap in Java classMinHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMinHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize + 1]; heapData[0] = Integer.MIN_VALUE; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return position / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position >= (sizeOfHeap / 2) && position heapData[getLeftChildPosition(position)] || heapData[position] >heapData[getRightChildPosition(position)]) { // swap with left child and then heapify the left child if (heapData[getLeftChildPosition(position)] = heapMaxSize) { return; } heapData[++sizeOfHeap] = data; int current = sizeOfHeap; while (heapData[current] <heapdata[getparentposition(current)]) { swap(current, getparentposition(current)); current="getParentPosition(current);" } crreatedisplayheap() method to print the data of heap public void displayheap() system.out.println('parent node' + ' ' 'left child 'right node'); for (int k="1;" position--) minheapify(position); create removeroot() removing minimum element from publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" minheapify(front); returnpopelement; minheapjavaimplementation class in java classminheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println('enter size min heap'); heapsize="sc.nextInt();" minheapheapobj="new" minheap(heapsize); for(inti="1;" i<="heapSize;" i++) system.out.print('enter '+i+' element: '); int heapobj.insertnode(data); close obj sc.close(); construct a given heapobj.designminheap(); display system.out.println('the is heapobj.displayheap(); root node system.out.println('after element(root node) '+heapobj.removeroot()+', is:'); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-2.webp" alt="Heap implementation in Java"> <h2>Max heap</h2> <p>Max heap is another special type of heap data structure that is also a complete binary tree in itself in Java. Max heap has the following properties:</p> <ol class="points"> <li>Root node value is always greater in comparison to the other nodes of the heap.</li> <li>Each internal node has a key value that is always greater or equal to its children.</li> </ol> <p>We can perform the following three operations in Max heap:</p> <h3>insertNode()</h3> <p>We can perform insertion in the Max heap by adding a new key at the end of the tree. If the value of the inserted key is greater than its parent node, we have to traverse the key upwards for fulfilling the heap property. The insertion process takes O(log n) time.</p> <h3>extractMax()</h3> <p>It is one of the most important operations which we perform to remove the maximum value node, i.e., the root node of the heap. After removing the root node, we have to make sure that heap property should be maintained. The extractMax() operation takes O(Log n) time to remove the maximum element from the heap.</p> <h3>getMax()</h3> <p>The <strong>getMax()</strong> operation is used to get the root node of the heap, i.e., maximum element in O(1) time.</p> <p> <strong>Example:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-3.webp" alt="Heap implementation in Java"> <p> <strong>Min heap Algorithm</strong> </p> <pre> proceduredesign_max_heap Array arr: of size n => array of elements // call min_heapify procedure for each element of the array to form max heap repeat for (k = n/2 ; k >= 1 ; k--) call procedure max_heapify (arr, k); proceduremin_heapify (vararr[ ] , var k, varn) { varleft_child = 2*k + 1; varright_child = 2*k+ 2; if(left_childarr[ largest ] ) largest = left_child; else largest = k; if(right_childarr[largest] ) largest = right_child; if(largest != k) { swaparr[ k ] and arr[ largest ]); callmax_heapify (arr, largest, n); } } </pre> <p> <strong>MaxHeapJavaImplementation.java</strong> </p> <pre> //import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; //create class MinHeap to construct Min heap in Java classMaxHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMaxHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize]; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return (position - 1) / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position > (sizeOfHeap / 2) && position <= sizeofheap) { return true; } false; create swapnodes() method that perform swapping of the given nodes heap firstnode and secondnode are positions private void swap(intfirstnode, intsecondnode) int temp; temp="heapData[firstNode];" heapdata[firstnode]="heapData[secondNode];" heapdata[secondnode]="temp;" maxheapify() to heapify node for maintaining property maxheapify(int position) check whether is non-leaf greater than its right left child if (!checkleaf(position)) (heapdata[position] <heapdata[getleftchildposition(position)] || heapdata[position] heapdata[getrightchildposition(position)]) swap(position, getleftchildposition(position)); maxheapify(getleftchildposition(position)); swap with else getrightchildposition(position)); maxheapify(getrightchildposition(position)); insertnode() insert element in public insertnode(int data) heapdata[sizeofheap]="data;" current="sizeOfHeap;" while (heapdata[current]>heapData[getParentPosition(current)]) { swap(current, getParentPosition(current)); current = getParentPosition(current); } sizeOfHeap++; } // create displayHeap() method to print the data of the heap public void displayHeap() { System.out.println('PARENT NODE' + ' ' + 'LEFT CHILD NODE' + ' ' + 'RIGHT CHILD NODE'); for (int k = 0; k <sizeofheap 2; k++) { system.out.print(' ' + heapdata[k] ' ' heapdata[2 * k 1] 2]); system.out.println(); } create designmaxheap() method to construct min heap public void for (int position="0;" < (sizeofheap 2); position++) maxheapify(position); removeroot() removing maximum element from the publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" maxheapify(front); returnpopelement; minheapjavaimplementation class in java classmaxheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println('enter size of max heap'); heapsize="sc.nextInt();" maxheapheapobj="new" maxheap(50); for(inti="1;" i<="heapSize;" i++) system.out.print('enter '+i+' element: '); int data="sc.nextInt();" heapobj.insertnode(data); close obj sc.close(); a given heapobj.designmaxheap(); display system.out.println('the is heapobj.displayheap(); root node system.out.println('after element(root node) '+heapobj.removeroot()+', is:'); pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-4.webp" alt="Heap implementation in Java"> <hr></sizeofheap></=></pre></heapdata[getparentposition(current)])></pre></=> MaxHeapJavaImplementation.java
//import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; //create class MinHeap to construct Min heap in Java classMaxHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMaxHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize]; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return (position - 1) / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position > (sizeOfHeap / 2) && position <= sizeofheap) { return true; } false; create swapnodes() method that perform swapping of the given nodes heap firstnode and secondnode are positions private void swap(intfirstnode, intsecondnode) int temp; temp="heapData[firstNode];" heapdata[firstnode]="heapData[secondNode];" heapdata[secondnode]="temp;" maxheapify() to heapify node for maintaining property maxheapify(int position) check whether is non-leaf greater than its right left child if (!checkleaf(position)) (heapdata[position] <heapdata[getleftchildposition(position)] || heapdata[position] heapdata[getrightchildposition(position)]) swap(position, getleftchildposition(position)); maxheapify(getleftchildposition(position)); swap with else getrightchildposition(position)); maxheapify(getrightchildposition(position)); insertnode() insert element in public insertnode(int data) heapdata[sizeofheap]="data;" current="sizeOfHeap;" while (heapdata[current]>heapData[getParentPosition(current)]) { swap(current, getParentPosition(current)); current = getParentPosition(current); } sizeOfHeap++; } // create displayHeap() method to print the data of the heap public void displayHeap() { System.out.println('PARENT NODE' + ' ' + 'LEFT CHILD NODE' + ' ' + 'RIGHT CHILD NODE'); for (int k = 0; k <sizeofheap 2; k++) { system.out.print(\' \' + heapdata[k] \' \' heapdata[2 * k 1] 2]); system.out.println(); } create designmaxheap() method to construct min heap public void for (int position="0;" < (sizeofheap 2); position++) maxheapify(position); removeroot() removing maximum element from the publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" maxheapify(front); returnpopelement; minheapjavaimplementation class in java classmaxheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println(\'enter size of max heap\'); heapsize="sc.nextInt();" maxheapheapobj="new" maxheap(50); for(inti="1;" i<="heapSize;" i++) system.out.print(\'enter \'+i+\' element: \'); int data="sc.nextInt();" heapobj.insertnode(data); close obj sc.close(); a given heapobj.designmaxheap(); display system.out.println(\'the is heapobj.displayheap(); root node system.out.println(\'after element(root node) \'+heapobj.removeroot()+\', is:\'); pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-4.webp" alt="Heap implementation in Java"> <hr></sizeofheap></=>