Dinamičko programiranje je tehnika koja rastavlja probleme u podprobleme i sprema rezultat za buduće potrebe tako da ne moramo ponovno izračunavati rezultat. Podproblemi su optimizirani za optimizaciju cjelokupnog rješenja, što je poznato kao svojstvo optimalne podstrukture. Glavna upotreba dinamičkog programiranja je rješavanje problema optimizacije. Ovdje problemi optimizacije znače kada pokušavamo pronaći minimalno ili maksimalno rješenje problema. Dinamičko programiranje jamči pronalaženje optimalnog rješenja problema ako rješenje postoji.

Definicija dinamičkog programiranja kaže da je to tehnika za rješavanje složenog problema tako da se prvo uđe u zbirku jednostavnijih podproblema, rješavajući svaki podproblem samo jednom, a zatim pohranjujući njihova rješenja kako bi se izbjegla ponavljajuća izračunavanja.

Razumimo ovaj pristup kroz primjer.

Razmotrimo primjer Fibonaccijevog niza. Sljedeći niz je Fibonaccijev niz:

program java

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…

Brojevi u gornjem nizu nisu nasumično izračunati. Matematički, mogli bismo napisati svaki od pojmova koristeći donju formulu:

F(n) = F(n-1) + F(n-2),

S osnovnim vrijednostima F(0) = 0 i F(1) = 1. Da bismo izračunali ostale brojeve, slijedimo gornji odnos. Na primjer, F(2) je zbroj f(0) i f(1), što je jednako 1.

Kako možemo izračunati F(20)?

F(20) član će se izračunati pomoću n-te formule Fibonaccijevog niza. Donja slika pokazuje kako se izračunava F(20).

semantička greška

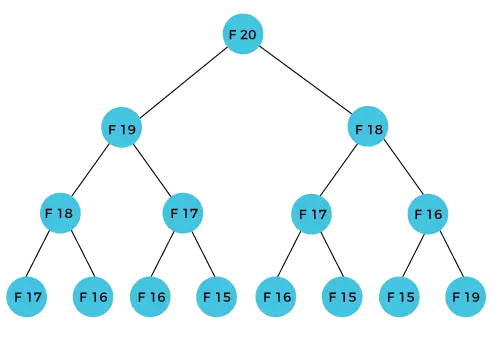
Kao što možemo vidjeti na gornjoj slici, F(20) se izračunava kao zbroj F(19) i F(18). U pristupu dinamičkog programiranja pokušavamo podijeliti problem na slične podprobleme. Ovaj pristup slijedimo u gornjem slučaju gdje F(20) prelazi u slične podprobleme, tj. F(19) i F(18). Ako ponovimo definiciju dinamičkog programiranja, ona kaže da se sličan podproblem ne smije izračunavati više od jednom. Ipak, u gornjem slučaju, podproblem se izračunava dva puta. U gornjem primjeru, F(18) se izračunava dva puta; slično, F(17) se također izračunava dvaput. Međutim, ova tehnika je vrlo korisna jer rješava slične podprobleme, ali moramo biti oprezni prilikom pohranjivanja rezultata jer nismo posebni u pohranjivanju rezultata koji smo izračunali jednom, a onda to može dovesti do rasipanja resursa.

U gornjem primjeru, ako izračunamo F(18) u desnom podstablu, to dovodi do ogromne upotrebe resursa i smanjuje ukupnu izvedbu.

Rješenje gornjeg problema je spremanje izračunatih rezultata u nizu. Prvo izračunavamo F(16) i F(17) i spremamo njihove vrijednosti u niz. F(18) se izračunava zbrajanjem vrijednosti F(17) i F(16), koje su već spremljene u nizu. Izračunata vrijednost F(18) sprema se u polje. Vrijednost F(19) izračunava se korištenjem zbroja F(18) i F(17), a njihove su vrijednosti već spremljene u nizu. Izračunata vrijednost F(19) pohranjuje se u nizu. Vrijednost F(20) može se izračunati zbrajanjem vrijednosti F(19) i F(18), a vrijednosti i F(19) i F(18) pohranjuju se u polje. Konačna izračunata vrijednost F(20) pohranjuje se u nizu.

Kako funkcionira pristup dinamičkog programiranja?

Slijede koraci koje slijedi dinamičko programiranje:

• Rastavlja složeni problem na jednostavnije podprobleme.
• Pronalazi optimalno rješenje za te podprobleme.
• Pohranjuje rezultate podproblema (memoizacija). Proces pohranjivanja rezultata podproblema poznat je kao memoriranje.
• Ponovno ih koristi tako da se isti podproblem izračunava više puta.
• Na kraju izračunajte rezultat složenog problema.

Gornjih pet koraka su osnovni koraci za dinamičko programiranje. Primjenjivo je dinamičko programiranje koje ima svojstva kao što su:

objekt jsonobject java

Oni problemi koji imaju preklapajuće podprobleme i optimalne podstrukture. Ovdje optimalna podstruktura znači da se rješenje optimizacijskih problema može dobiti jednostavnom kombinacijom optimalnog rješenja svih podproblema.

U slučaju dinamičkog programiranja, prostorna složenost bi bila povećana jer pohranjujemo međurezultate, ali bi vremenska složenost bila smanjena.

Pristupi dinamičkog programiranja

Postoje dva pristupa dinamičkom programiranju:

• Pristup odozgo prema dolje
• Pristup odozdo prema gore

Pristup odozgo prema dolje

Pristup odozgo prema dolje slijedi tehniku ​​memoriranja, dok pristup odozdo prema gore slijedi metodu tabličnog prikaza. Ovdje je memoriranje jednako zbroju rekurzije i predmemoriranja. Rekurzija znači pozivanje same funkcije, dok keširanje znači pohranjivanje međurezultata.

čitati Excel datoteku u Javi

Prednosti

• Vrlo je lako razumjeti i implementirati.
• Rješava podprobleme samo kada je to potrebno.
• Lako je otkloniti pogreške.

Nedostaci

Koristi tehniku ​​rekurzije koja zauzima više memorije u stogu poziva. Ponekad kada je rekurzija preduboka, dogodit će se stanje preljeva stoga.

Zauzima više memorije što degradira ukupnu izvedbu.

Razmotrimo dinamičko programiranje kroz primjer.

 int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of &apos;n&apos; increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td>  </tr><tr><td>Bottom-Up</td>  </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let&apos;s understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let&apos;s understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>