U ovom odjeljku raspravljat ćemo o metodi pretvaranja NFA u njegov ekvivalent DFA. U NFA, kada se određeni unos da trenutnom stanju, stroj prelazi u višestruka stanja. Može imati nula, jedan ili više od jednog poteza na danom ulaznom simbolu. S druge strane, u DFA-u, kada se da određeni unos trenutnom stanju, stroj prelazi u samo jedno stanje. DFA ima samo jedan potez na danom ulaznom simbolu.
Neka je M = (Q, ∑, δ, q0, F) NFA koji prihvaća jezik L(M). Trebao bi postojati ekvivalentni DFA označen s M' = (Q', ∑', q0', δ', F') tako da je L(M) = L(M').
Koraci za pretvaranje NFA u DFA:
Korak 1: U početku Q' = ϕ
Korak 2: Dodajte q0 NFA u Q'. Zatim pronađite prijelaze iz ovog početnog stanja.
Korak 3: U Q' pronađite mogući skup stanja za svaki ulazni simbol. Ako ovaj skup stanja nije u Q', dodajte ga u Q'.
bash while petlja
Korak 4: U DFA, konačno stanje će biti sva stanja koja sadrže F (konačna stanja NFA)
Primjer 1:
Pretvorite navedeni NFA u DFA.
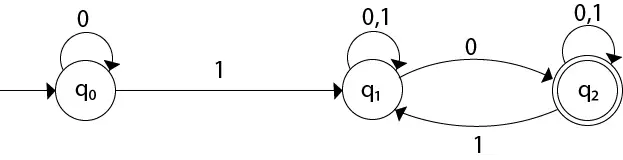
Riješenje: Za navedeni prijelazni dijagram prvo ćemo konstruirati prijelaznu tablicu.
| država | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Sada ćemo dobiti δ' prijelaz za stanje q0.
program java
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
Prijelaz δ' za stanje q1 dobiva se kao:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
Prijelaz δ' za stanje q2 dobiva se kao:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Sada ćemo dobiti δ' prijelaz na [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] Stanje [q1, q2] također je konačno stanje jer sadrži konačno stanje q2. Prijelazna tablica za konstruirani DFA bit će:
datum pretvoriti u niz
| država | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
Dijagram tranzicije će biti:

Stanje q2 se može eliminirati jer je q2 nedostižno stanje.
Primjer 2:
Pretvorite navedeni NFA u DFA.

Riješenje: Za navedeni prijelazni dijagram prvo ćemo konstruirati prijelaznu tablicu.
java niz bajtova u niz
| država | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Sada ćemo dobiti δ' prijelaz za stanje q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] Prijelaz δ' za stanje q1 dobiva se kao:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Sada ćemo dobiti δ' prijelaz na [q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] Slično tome,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Kako je u danom NFA, q1 konačno stanje, tada u DFA gdje god postoji q1 to stanje postaje konačno stanje. Stoga su u DFA konačna stanja [q1] i [q0, q1]. Stoga je skup konačnih stanja F = {[q1], [q0, q1]}.
avl stabla
Prijelazna tablica za konstruirani DFA bit će:
| država | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
Dijagram tranzicije će biti:

Čak i mi možemo promijeniti nazive država DFA.
Pretpostavimo
A = [q0] B = [q1] C = [q0, q1]
S ovim novim imenima DFA će biti kako slijedi:

