• Pushdown automata način je implementacije CFG-a na isti način na koji dizajniramo DFA za običnu gramatiku. DFA može zapamtiti konačnu količinu informacija, ali PDA može zapamtiti beskonačnu količinu informacija.
• Pushdown automata jednostavno je NFA proširen s 'vanjskom memorijom skupa'. Dodavanje stoga koristi se za pružanje mogućnosti upravljanja memorijom po principu 'zadnji-ušao-prvi-vani' Pushdown automatima. Pushdown automati mogu pohraniti neograničenu količinu informacija na stog. Može pristupiti ograničenoj količini informacija na stogu. PDA može gurnuti element na vrh hrpe i iskočiti element s vrha hrpe. Za čitanje elementa u stog, gornji elementi moraju biti iskočeni i izgubljeni su.
• PDA je moćniji od FA. Svaki jezik koji može biti prihvatljiv za FA može također biti prihvatljiv za PDA. PDA također prihvaća klasu jezika koju ne može prihvatiti čak ni FA. Stoga je PDA mnogo superiorniji od FA.

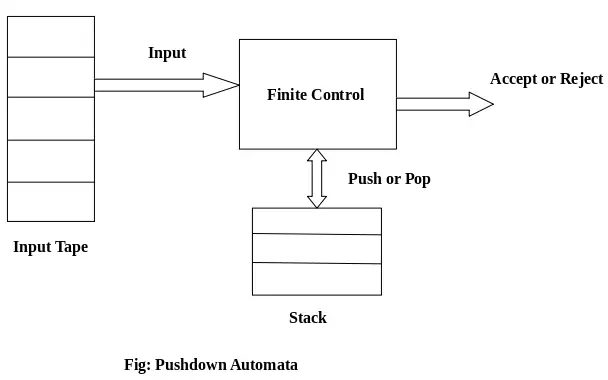
PDA komponente:

Ulazna traka: Ulazna vrpca podijeljena je na mnogo ćelija ili simbola. Glava za unos je samo za čitanje i može se pomicati samo slijeva nadesno, jedan po jedan simbol.

Konačna kontrola: Konačna kontrola ima neki pokazivač koji pokazuje trenutni simbol koji treba pročitati.

Stog: Hrpa je struktura u koju možemo gurati i uklanjati stavke samo s jednog kraja. Ima beskonačnu veličinu. U PDA, stog se koristi za privremeno spremanje stavki.

Formalna definicija PDA:

PDA se može definirati kao skup od 7 komponenti:

P: konačan skup stanja

∑: ulazni skup

C: simbol hrpe koji se može gurnuti i iskočiti iz hrpe

q0: početno stanje

tranzicija neprozirnosti css

S: početni simbol koji je u Γ.

F: skup konačnih stanja

d: funkcija mapiranja koja se koristi za prelazak iz trenutnog stanja u sljedeće stanje.

Trenutačni opis (ID)

ID je neformalni zapis o tome kako PDA računa ulazni niz i donosi odluku da li je niz prihvaćen ili odbijen.

Trenutačni opis je trojka (q, w, α) gdje je:

q opisuje trenutno stanje.

U opisuje preostali unos.

do i while petlja u Javi

a opisuje sadržaj hrpe, gore lijevo.

Oznaka skretnice:

Znak ⊢ opisuje oznaku okretnice i predstavlja jedan potez.

⊢* znak opisuje niz poteza.

Na primjer,

(p, b, T) ⊢ (q, w, α)

strojopis za svaki

U gornjem primjeru, tijekom prijelaza iz stanja p u q, ulazni simbol 'b' se troši, a vrh hrpe 'T' predstavljen je novim nizom α.

Primjer 1:

Dizajnirajte PDA za prihvaćanje jezika aⁿb²ⁿ.

Riješenje: U ovom jeziku iza n broja a treba slijediti 2n broja b-a. Stoga ćemo primijeniti vrlo jednostavnu logiku, a to je da ako pročitamo jedno 'a', gurnut ćemo dva a na stog. Čim pročitamo 'b' tada za svako pojedino 'b' samo jedno 'a' treba iskočiti iz hrpe.

ID se može konstruirati na sljedeći način:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Sada kada čitamo b, promijenit ćemo stanje iz q0 u q1 i početi iskakati odgovarajuće 'a'. Stoga,

 δ(q0, b, a) = (q1, ε) 

Stoga će se ovaj proces iskakanja 'b' ponavljati osim ako se ne pročitaju svi simboli. Imajte na umu da se radnja iskakanja događa samo u stanju q1.

 δ(q1, b, a) = (q1, ε) 

Nakon čitanja svih b-ova, sva odgovarajuća a-a trebala bi se iskočiti. Prema tome, kada čitamo ε kao ulazni simbol, tada ne bi trebalo biti ničega u stogu. Stoga će potez biti:

 δ(q1, ε, Z) = (q2, ε) 

Gdje

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

ID možemo sažeti kao:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Sada ćemo simulirati ovaj PDA za ulazni niz 'aaabbbbbb'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Primjer 2:

Dizajnirajte PDA za prihvaćanje jezika 0ⁿ1^m0ⁿ.

Riješenje: U ovom PDA-u, n od 0 slijedi bilo koji broj 1 nakon n od 0. Stoga će logika za dizajn takvog PDA biti sljedeća:

Gurnite sve nule na hrpu kad naiđete na prve nule. Zatim, ako čitamo 1, jednostavno ne činimo ništa. Zatim pročitajte 0 i pri svakom očitanju 0 izvucite jednu 0 iz hrpe.

koliko nula za jedan milijun

Na primjer:

Ovaj scenarij može se napisati u ID obliku kao:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Sada ćemo simulirati ovaj PDA za ulazni niz '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT