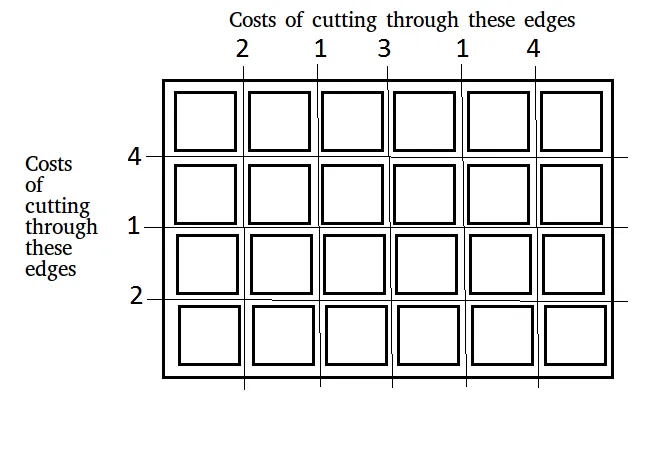
S obzirom na ploču dimenzija n × m koju treba izrezati na n × m kvadrata. Troškovi rezanja duž vodoravnog ili okomitog ruba navedeni su u dva niza:

• x[] : Rezanje troškova duž okomitih rubova (po dužini).
• i[] : Rezanje troškova duž horizontalnih rubova (po širini).

Pronađite minimalni ukupni trošak potreban za optimalno rezanje ploče na kvadrate.

Primjeri: 

Ulazni: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Izlaz: 42
Obrazloženje:

U početku br. horizontalnih segmenata = 1 & br. okomitih segmenata = 1.
Optimalan način rezanja na kvadrat je:
Odaberite 4 (od x) -> okomiti rez Trošak = 4 × vodoravni segmenti = 4
 Sada vodoravni segmenti = 1 okomiti segmenti = 2.
Odaberite 4 (od y) -> vodoravni rez Trošak = 4 × okomiti segmenti = 8
 Sada vodoravni segmenti = 2 okomita segmenta = 2.
Odaberite 3 (od x) -> okomiti rez Cijena = 3 × vodoravni segmenti = 6
 Sada vodoravni segmenti = 2 okomita segmenta = 3.
Odaberite 2 (od x) -> okomiti rez Trošak = 2 × vodoravni segmenti = 4
 Sada vodoravni segmenti = 2 okomita segmenta = 4.
Odaberite 2 (od y) -> vodoravni rez Trošak = 2 × okomiti segmenti = 8
 Sada vodoravni segmenti = 3 okomita segmenta = 4.
Odaberite 1 (od x) -> okomiti rez Cijena = 1 × vodoravni segmenti = 3
Sada vodoravni segmenti = 3 okomita segmenta = 5.
Odaberite 1 (od x) -> okomiti rez Cijena = 1 × vodoravni segmenti = 3
Sada vodoravni segmenti = 3 okomita segmenta = 6.
Odaberite 1 (od y) -> vodoravni rez Trošak = 1 × okomiti segmenti = 6
Sada vodoravni segmenti = 4 okomita segmenta = 6.
Dakle, ukupni trošak = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Ulazni: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Izlaz: 15
Obrazloženje:
U početku br. horizontalnih segmenata = 1 & br. okomitih segmenata = 1.
Optimalan način rezanja na kvadrat je:
Odaberite 1 (od y) -> vodoravni rez Trošak = 1 × okomiti segmenti = 1
Sada vodoravni segmenti = 2 okomita segmenta = 1.
Odaberite 1 (od y) -> vodoravni rez Trošak = 1 × okomiti segmenti = 1
Sada vodoravni segmenti = 3 okomita segmenta = 1.
Odaberite 1 (od y) -> vodoravni rez Trošak = 1 × okomiti segmenti = 1
Sada vodoravni segmenti = 4 okomita segmenta = 1.
Odaberite 1 (od x) -> okomiti rez Cijena = 1 × vodoravni segmenti = 4
Sada vodoravni segmenti = 4 okomita segmenta = 2.
Odaberite 1 (od x) -> okomiti rez Cijena = 1 × vodoravni segmenti = 4
Sada vodoravni segmenti = 4 okomita segmenta = 3.
Odaberite 1 (od x) -> okomiti rez Cijena = 1 × vodoravni segmenti = 4
Sada vodoravni segmenti = 4 okomita segmenta = 4
Dakle, ukupni trošak = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Sadržaj

• [Naivni pristup] Isprobajte sve permutacije - O((n+m)!×(n+m)) vrijeme i O(n+m) prostor
• [Očekivani pristup] Korištenje pohlepne tehnike - O( n (log n)+m (log m)) vrijeme i O(1) prostor

[Naivni pristup] Isprobajte sve permutacije - O((n+m)!×(n+m)) vrijeme i O(n+m) prostor

Ideja je generirati sve moguće permutacije zadanih rezova i zatim izračunati trošak za svaku permutaciju. Konačno vratite minimalne troškove među njima.

Bilješka: Ovaj pristup nije izvediv za veće ulaze jer broj permutacija faktorijelno raste kao (m+n-2)!.
Za svaku permutaciju moramo izračunati trošak u O(m+n) vremenu. Stoga ukupna vremenska složenost postaje O((m+n−2)!×(m+n)).

[Očekivani pristup] Korištenje pohlepne tehnike - O( n (log n)+m (log m)) vrijeme i O(1) prostor

Ideja je prvo napraviti najskuplje rezove pomoću a pohlepan pristup . Opažanje je da odabir najvećeg smanjenja troškova u svakom koraku smanjuje buduće troškove utječući na više komada odjednom. Troškove okomitog (x) i vodoravnog (y) smanjenja sortiramo silaznim redoslijedom, a zatim iterativno odabiremo veći kako bismo maksimizirali uštede troškova. Preostali rezovi obrađuju se zasebno kako bi se osiguralo da su svi dijelovi optimalno podijeljeni.

Što se događa kada napravimo rez?

• Horizontalni rez → režete po širini tako da se broj horizontalnih traka povećava (hCount++). Ali trošak se množi s vCount (broj okomitih traka) jer vodoravni rez mora proći kroz sve okomite segmente.
• Vertikalni rez → režete po visini tako da se broj okomitih traka povećava (vCount++). Ali trošak se množi s hCount (broj vodoravnih traka) jer okomiti rez mora proći kroz sve vodoravne segmente.

Koraci za rješavanje problema:

• Poredaj nizove x i y silaznim redoslijedom.
• Koristite dva pokazivača, jedan za x i jedan za y, počevši od najveće vrijednosti i krećući se prema manjim vrijednostima.
• Održavajte hCount i vCount da biste pratili na koliko segmenata svaki rez utječe i ažurirajte ih u skladu s tim.
• Ponavljajte dok i x i y imaju neobrađene rezove uvijek birajući veći trošak kako biste smanjili ukupne troškove.
• Ako x ima preostale rezove, obradite ih multiplikatorom hCount ; na sličan način obradite preostale y rezove s vCount.
• Akumulirajte ukupni trošak u svakom koraku pomoću formule: smanjite trošak * broj zahvaćenih komada osiguravajući minimalni trošak.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42