logo

TechCodeview

Najveći broj u BST koji je manji ili jednak k

S obzirom na korijen od a Stablo binarnog pretraživanja i cijeli broj k . Zadatak je pronaći najveći broj u stablu binarnog pretraživanja koje je manje od ili jednak do k ako takav element ne postoji ispišite -1. 

Primjeri:  

Ulazni:



Najveći-broj-u-BST-koji-je-manji-od-ili-jednak-k-1' title=

Izlaz: 21
Objašnjenje: 19 i 25 su dva najbliža broja 21, a 19 je najveći broj koji ima vrijednost manju ili jednaku 21.

Ulazni: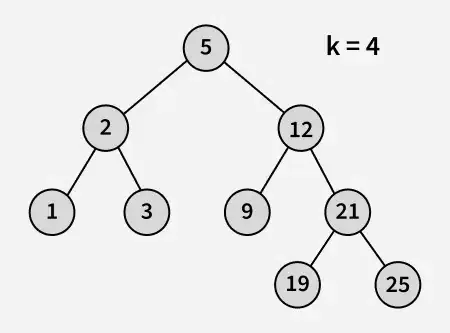

Najveći-broj-u-BST-koji-je-manji-od-ili-jednak-k-2' loading='lazy' title=

Izlaz: 3
Objašnjenje: 3 i 5 su dva najbliža broja 4, a 3 je najveći broj koji ima vrijednost manju ili jednaku 4.

Sadržaj

[Naivni pristup] Korištenje rekurzije - O(h) vrijeme i O(h) prostor

korijen i usporedite njegovu vrijednost s k. Ako je vrijednost čvora veća od k, prijeđite na lijevo podstablo. Inače pronađite vrijednost najvećeg broja manjeg od jednakog k u desno podstablo . Ako desno podstablo vrati -1 (što znači da takva vrijednost ne postoji), tada vraća vrijednost trenutnog čvora. Inače vraća vrijednost koju vraća desno podstablo (jer će biti veća od vrijednosti trenutnog čvora, ali manja od jednake k).

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    // Base cases  if (root == nullptr)  return -1;  if (root->data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root->data < k) {    int x = findMaxFork(root->right k);  if (x == -1)  return root->data;  else  return x;  }  // If root's data is greater   // return value from left subtree.  return findMaxFork(root->left k);  } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = findMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k);  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): # Base cases if root is None: return -1 if root.data == k: return k # If root's value is smaller # try in right subtree elif root.data < k: x = findMaxFork(root.right k) if x == -1: return root.data else: return x # If root's data is greater # return value from left subtree. return findMaxFork(root.left k) if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = FindMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return FindMaxFork(root.left k);  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {    // Base cases  if (root === null)  return -1;  if (root.data === k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  let x = findMaxFork(root.right k);  if (x === -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k); } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Izlaz 
21

[Očekivani pristup] Korištenje iteracije - O(h) vrijeme i O(1) prostor

Ideja je početi od korijen i usporediti njegovu vrijednost s k . Ako je vrijednost čvora <= k ažurirajte vrijednost rezultata na korijensku vrijednost i pomaknite se na pravo podstablo inače premjestiti na lijevo podstablo. Po iterativno primjenom ove operacije na sve čvorove možemo minimizirati prostor potreban za rekurzija stog.

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    int result = -1;    // Start from root and keep looking for larger   while (root != nullptr) {  // If root is smaller go to right side  if (root->data <= k){  result = root->data;  root = root->right;  }  // If root is greater go to left side   else  root = root->left;  }    return result; } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): result = -1 # Start from root and keep looking for larger  while root is not None: # If root is smaller go to right side if root.data <= k: result = root.data root = root.right # If root is greater go to left side  else: root = root.left return result if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {  let result = -1;    // Start from root and keep looking for larger   while (root !== null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result; } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Izlaz 
21
Napravi kviz