Pohlepna metoda jedna je od strategija poput Podijeli pa vladaj koja se koristi za rješavanje problema. Ova metoda se koristi za rješavanje problema optimizacije. Optimizacijski problem je problem koji zahtijeva maksimalne ili minimalne rezultate. Shvatimo kroz neke pojmove.
Greedy metoda je najjednostavniji i izravniji pristup. To nije algoritam, ali je tehnika. Glavna funkcija ovog pristupa je da se odluka donosi na temelju trenutno dostupnih informacija. Kakve god trenutne informacije bile prisutne, odluka se donosi bez brige o učinku trenutne odluke u budućnosti.
spojevi i vrste spojeva
Ova se tehnika u osnovi koristi za određivanje izvedivog rješenja koje može, ali i ne mora biti optimalno. Izvedivo rješenje je podskup koji zadovoljava zadane kriterije. Optimalno rješenje je ono rješenje koje je najbolje i najpovoljnije rješenje u podskupu. U slučaju izvedivih, ako više od jednog rješenja zadovoljava zadane kriterije tada će se ta rješenja smatrati izvedivima, dok je optimalno rješenje najbolje rješenje među svim rješenjima.
Karakteristike Greedy metode
Sljedeće su karakteristike pohlepne metode:
- Kako bi se rješenje konstruiralo na optimalan način, ovaj algoritam kreira dva skupa od kojih jedan skup sadrži sve odabrane stavke, a drugi skup sadrži odbijene stavke.
- Greedy algoritam donosi dobre lokalne izbore u nadi da bi rješenje trebalo biti izvedivo ili optimalno.
Komponente pohlepnog algoritma
Komponente koje se mogu koristiti u pohlepnom algoritmu su:
povijest verzija androida
Primjene pohlepnog algoritma
- Koristi se za pronalaženje najkraćeg puta.
- Koristi se za pronalaženje minimalnog razapinjućeg stabla pomoću Primovog algoritma ili Kruskalovog algoritma.
- Koristi se u redoslijedu poslova s rokom.
- Ovaj se algoritam također koristi za rješavanje problema frakcijskog naprtnjače.
Pseudo kod pohlepnog algoritma
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Gore navedeno je pohlepni algoritam. U početku se rješenju dodjeljuje nula vrijednost. Prosljeđujemo niz i broj elemenata u pohlepnom algoritmu. Unutar for petlje odabiremo jedan po jedan element i provjeravamo je li rješenje izvedivo ili nije. Ako je rješenje izvedivo, tada izvodimo uniju.
Shvatimo kroz primjer.
Pretpostavimo da postoji problem 'P'. Želim putovati od A do B kako je prikazano u nastavku:
P: A → B
Problem je u tome što moramo prijeći ovo putovanje od A do B. Postoje različita rješenja za odlazak od A do B. Možemo ići od A do B hodati, auto, bicikl, vlak, avion , itd. Postoji ograničenje u putovanju da ovo putovanje moramo prijeći unutar 12 sati. Samo ako idem vlakom ili avionom, tu udaljenost mogu prijeći za 12 sati. Postoji mnogo rješenja za ovaj problem, ali postoje samo dva rješenja koja zadovoljavaju ograničenje.
git dodaj sve
Ako kažemo da moramo preći put uz minimalne troškove. To znači da tu udaljenost moramo prijeći što je moguće manje, pa je ovaj problem poznat kao problem minimizacije. Za sada imamo dva izvediva rješenja, jedno vlakom i drugo zrakoplovom. Budući da će putovanje vlakom dovesti do minimalnih troškova, to je optimalno rješenje. Optimalno rješenje također je izvedivo rješenje, ali pruža najbolji rezultat tako da je to rješenje optimalno rješenje uz minimalne troškove. Postojalo bi samo jedno optimalno rješenje.
Problem koji zahtijeva ili minimalni ili maksimalni rezultat je poznat kao problem optimizacije. Greedy metoda je jedna od strategija koja se koristi za rješavanje problema optimizacije.
Nedostaci korištenja Greedy algoritma
Pohlepni algoritam donosi odluke na temelju informacija dostupnih u svakoj fazi bez razmatranja šireg problema. Dakle, može postojati mogućnost da pohlepno rješenje ne daje najbolje rješenje za svaki problem.
Slijedi lokalni optimalni izbor u svakoj fazi s namjerom pronalaska globalnog optimuma. Shvatimo kroz primjer.
Razmotrite grafikon koji je dan u nastavku:
c# primjeri koda
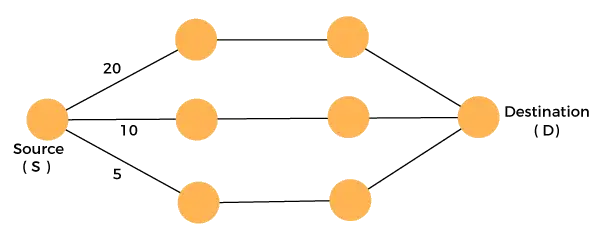
Moramo putovati od izvora do odredišta uz minimalne troškove. Budući da imamo tri izvediva rješenja koja imaju troškovne staze kao što su 10, 20 i 5. 5 je minimalna troškovna putanja, pa je to optimalno rješenje. Ovo je lokalni optimum i na taj način nalazimo lokalni optimum u svakoj fazi kako bismo izračunali globalno optimalno rješenje.
