Zadana je pravokutna matrica mat[][] gdje neke ćelije sadrže mine (označene s 0), a ostale su sigurne (označene s 1) pronađite duljinu najkraće sigurne rute od bilo koje ćelije u prvom stupcu do bilo koje ćelije u zadnjem stupcu.
- Nagazne mine nisu sigurne i njihove četiri susjedne ćelije (gore dolje lijevo desno) također nisu sigurne.
- Dopušteni su samo vodoravni i okomiti pomaci na susjedne sigurne ćelije.
- Ako je nemoguće doći do posljednjeg stupca sigurno vratite -1.
Primjeri:
Ulazni:
s [][] = [ [1 0 1 1 1]
[1 1 1 1 1]
[1 1 1 1 1]
[1 1 1 0 1]
[1 1 1 1 0] ]
Izlaz: 6
Obrazloženje:
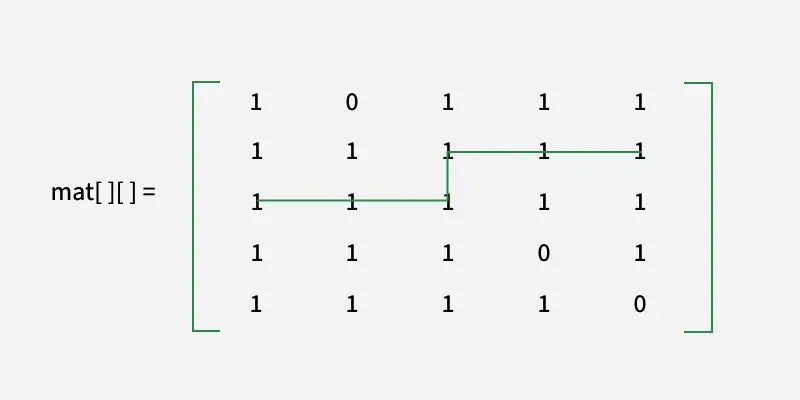
Možemo vidjeti tu duljinu najkraćeg
siguran put je 6.
Ulazni:
s [][] = [ [1 1 1 1 1]
[1 1 0 1 1]
[1 1 1 1 1] ]
Izlaz: -1
Obrazloženje: Ne postoji mogući put od
prvi stupac do zadnjeg stupca.
Sadržaj
[Pristup] Korištenje povratnog praćenja
C++Ideja je koristiti Povratak . Prvo označimo sve susjedne ćelije nagaznih mina kao nesigurne. Zatim se za svaku sigurnu ćeliju prvog stupca matrice krećemo naprijed u svim dopuštenim smjerovima i rekurzivno provjeravamo vode li do odredišta ili ne. Ako je odredište pronađeno, ažuriramo vrijednost najkraćeg puta, inače ako nijedno od gore navedenih rješenja ne radi, vraćamo false iz naše funkcije.
#include
import java.util.Arrays; class Solution { // Function to mark unsafe cells (landmines and their adjacent cells) private void markUnsafeCells(int[][] mat) { int r = mat.length; int c = mat[0].length; int[] row = {-1 1 0 0}; int[] col = {0 0 -1 1}; // Create a copy to avoid modifying original safe cells prematurely int[][] temp = new int[r][c]; for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { temp[i][j] = mat[i][j]; } } // Mark adjacent cells of landmines (0) as unsafe (0) for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { if (temp[i][j] == 0) { for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int dfs(int[][] mat boolean[][] visited int i int j int c) { int r = mat.length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] == 0 || visited[i][j]) { return Integer.MAX_VALUE; } if (j == c - 1) { return 1; } visited[i][j] = true; int[] row = {-1 1 0 0}; int[] col = {0 0 -1 1}; int minPath = Integer.MAX_VALUE; // Try all four directions for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; int pathLength = dfs(mat visited ni nj c); if (pathLength != Integer.MAX_VALUE) { minPath = Math.min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } public int findShortestPath(int[][] mat) { int r = mat.length; int c = mat[0].length; // Mark all adjacent cells of landmines as unsafe markUnsafeCells(mat); boolean[][] visited = new boolean[r][c]; int minPath = Integer.MAX_VALUE; // Try starting from each safe cell in the first column for (int i = 0; i < r; i++) { if (mat[i][0] == 1) { int pathLength = dfs(mat visited i 0 c); if (pathLength != Integer.MAX_VALUE) { minPath = Math.min(minPath pathLength); } } } return minPath == Integer.MAX_VALUE ? -1 : minPath; } public static void main(String[] args) { int[][] mat = { {1 0 1 1 1} {1 1 1 1 1} {1 1 1 1 1} {1 1 1 0 1} {1 1 1 1 0} }; Solution solution = new Solution(); int result = solution.findShortestPath(mat); System.out.println(result); } }
# Function to mark unsafe cells (landmines and their adjacent cells) def mark_unsafe_cells(mat): r = len(mat) c = len(mat[0]) # Directions for adjacent cells: up down left right row = [-1 1 0 0] col = [0 0 -1 1] # Create a copy to avoid modifying original safe cells prematurely temp = [row[:] for row in mat] # Mark adjacent cells of landmines (0) as unsafe (0) for i in range(r): for j in range(c): if temp[i][j] == 0: for k in range(4): ni = i + row[k] nj = j + col[k] if 0 <= ni < r and 0 <= nj < c: mat[ni][nj] = 0 # DFS to find shortest path from (i j) to any cell in last column def dfs(mat visited i j c): r = len(mat) # If out of bounds blocked or visited if i < 0 or i >= r or j < 0 or j >= c or mat[i][j] == 0 or visited[i][j]: return float('inf') if j == c - 1: return 1 visited[i][j] = True # Four possible moves: up down left right row = [-1 1 0 0] col = [0 0 -1 1] min_path = float('inf') # Try all four directions for k in range(4): ni = i + row[k] nj = j + col[k] path_length = dfs(mat visited ni nj c) if path_length != float('inf'): min_path = min(min_path 1 + path_length) # Backtrack - unmark current cell visited[i][j] = False return min_path def findShortestPath(mat): r = len(mat) c = len(mat[0]) # Mark all adjacent cells of landmines as unsafe mark_unsafe_cells(mat) visited = [[False] * c for _ in range(r)] min_path = float('inf') # Try starting from each safe cell in the first column for i in range(r): if mat[i][0] == 1: path_length = dfs(mat visited i 0 c) if path_length != float('inf'): min_path = min(min_path path_length) return -1 if min_path == float('inf') else min_path def main(): mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ] result = findShortestPath(mat) print(result) if __name__ == '__main__': main()
using System; class GFG { // Function to mark unsafe cells (landmines and their adjacent cells) private void MarkUnsafeCells(int[][] mat) { int r = mat.Length; int c = mat[0].Length; // Directions for adjacent cells: up down left right int[] row = { -1 1 0 0 }; int[] col = { 0 0 -1 1 }; // Create a copy to avoid modifying original safe cells prematurely int[][] temp = new int[r][]; for (int i = 0; i < r; i++) { temp[i] = new int[c]; Array.Copy(mat[i] temp[i] c); } // Mark adjacent cells of landmines (0) as unsafe (0) for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { if (temp[i][j] == 0) { for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int Dfs(int[][] mat bool[][] visited int i int j int c) { int r = mat.Length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] == 0 || visited[i][j]) { return int.MaxValue; } if (j == c - 1) { return 1; } visited[i][j] = true; int[] row = { -1 1 0 0 }; int[] col = { 0 0 -1 1 }; int minPath = int.MaxValue; // Try all four directions for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; int pathLength = Dfs(mat visited ni nj c); if (pathLength != int.MaxValue) { minPath = Math.Min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } public int FindShortestPath(int[][] mat) { int r = mat.Length; int c = mat[0].Length; // Mark all adjacent cells of landmines as unsafe MarkUnsafeCells(mat); bool[][] visited = new bool[r][]; for (int i = 0; i < r; i++) { visited[i] = new bool[c]; } int minPath = int.MaxValue; // Try starting from each safe cell in the first column for (int i = 0; i < r; i++) { if (mat[i][0] == 1) { int pathLength = Dfs(mat visited i 0 c); if (pathLength != int.MaxValue) { minPath = Math.Min(minPath pathLength); } } } return minPath == int.MaxValue ? -1 : minPath; } static void Main(string[] args) { int[][] mat = new int[][] { new int[] { 1 0 1 1 1 } new int[] { 1 1 1 1 1 } new int[] { 1 1 1 1 1 } new int[] { 1 1 1 0 1 } new int[] { 1 1 1 1 0 } }; GFG solution = new GFG(); int result = solution.FindShortestPath(mat); Console.WriteLine(result); } }
function markUnsafeCells(mat) { const r = mat.length; const c = mat[0].length; // Directions for adjacent cells: up down left right const row = [-1 1 0 0]; const col = [0 0 -1 1]; // Create a copy to avoid modifying original safe cells prematurely const temp = mat.map(row => [...row]); // Mark adjacent cells of landmines (0) as unsafe (0) for (let i = 0; i < r; i++) { for (let j = 0; j < c; j++) { if (temp[i][j] === 0) { for (let k = 0; k < 4; k++) { const ni = i + row[k]; const nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } function dfs(mat visited i j c) { const r = mat.length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] === 0 || visited[i][j]) { return Infinity; } // If reached the last column if (j === c - 1) { return 1; } visited[i][j] = true; const row = [-1 1 0 0]; const col = [0 0 -1 1]; let minPath = Infinity; // Try all four directions for (let k = 0; k < 4; k++) { const ni = i + row[k]; const nj = j + col[k]; const pathLength = dfs(mat visited ni nj c); if (pathLength !== Infinity) { minPath = Math.min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } function findShortestPath(mat) { const r = mat.length; const c = mat[0].length; // Mark all adjacent cells of landmines as unsafe markUnsafeCells(mat); const visited = Array(r).fill().map(() => Array(c).fill(false)); let minPath = Infinity; // Try starting from each safe cell in the first column for (let i = 0; i < r; i++) { if (mat[i][0] === 1) { const pathLength = dfs(mat visited i 0 c); if (pathLength !== Infinity) { minPath = Math.min(minPath pathLength); } } } return minPath === Infinity ? -1 : minPath; } const mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ]; const result = findShortestPath(mat); console.log(result);
Izlaz
6
Vremenska složenost: O(4^(r * c)) gdje je r broj redaka, a c broj stupaca u zadanoj matrici.
Pomoćni prostor: O(r * c) jer koristimo dodatni prostor poput visted[r][c].
[Optimizirani pristup] Korištenje pretraživanja u širinu
C++Može se riješiti u polinomijalnom vremenu koristeći Breadth-First Search. Stavite sve sigurne ćelije iz posljednjeg stupca u red čekanja s udaljenošću = 1. Kako BFS napreduje, izračunava se najkraći put do svake ćelije iz posljednjeg stupca. Na kraju između svih dostupnih ćelija u prvom stupcu ispišite minimalnu udaljenost.
#include
import java.util.*; public class Solution { static int[] rowNum = {-1 0 0 1}; static int[] colNum = {0 -1 1 0}; public static int findShortestPath(int[][] mat) { int n = mat.length; int m = mat[0].length; Queue<int[]> q = new LinkedList<>(); int[][] d = new int[n][m]; // Initializing distance array with large values for (int i = 0; i < n; i++) { Arrays.fill(d[i] (int) 1e9); } // Lambda-like helper function: check if cell is valid java.util.function.BiFunction<Integer Integer Boolean> isValid = (i j) -> { return !(i < 0 || i >= n || j < 0 || j >= m); }; // Helper function: check if cell and adjacent cells are safe java.util.function.BiFunction<Integer Integer Boolean> check = (i j) -> { if (!isValid.apply(i j)) return false; for (int k = 0; k < 4; k++) { int ni = i + rowNum[k]; int nj = j + colNum[k]; if (isValid.apply(ni nj) && mat[ni][nj] == 0) return false; } return true; }; // Pushing cells from the rightmost column into the queue for (int i = 0; i < n; i++) { if (check.apply(i m - 1)) { q.add(new int[]{i m - 1 1}); } } // BFS traversal while (!q.isEmpty()) { int[] z = q.poll(); int x = z[0] y = z[1] dis = z[2]; if (d[x][y] > dis) { d[x][y] = dis; for (int k = 0; k < 4; k++) { int ni = x + rowNum[k]; int nj = y + colNum[k]; if (check.apply(ni nj)) { q.add(new int[]{ni nj dis + 1}); } } } } // Finding the minimum distance in the first column int ans = (int) 1e9; for (int i = 0; i < n; i++) { ans = Math.min(ans d[i][0]); } // If no safe path found return -1 if (ans >= 1e9) ans = -1; return ans; } public static void main(String[] args) { int[][] mat = { {1 0 1 1 1} {1 1 1 1 1} {1 1 1 1 1} {1 1 1 0 1} {1 1 1 1 0} }; int result = findShortestPath(mat); System.out.println(result); } }
from collections import deque rowNum = [-1 0 0 1] colNum = [0 -1 1 0] def findShortestPath(mat): n = len(mat) m = len(mat[0]) q = deque() d = [[10**9 for _ in range(m)] for _ in range(n)] # Check if cell is valid def isValid(i j): return not (i < 0 or i >= n or j < 0 or j >= m) # Check if cell and its adjacent cells are safe def check(i j): if not isValid(i j): return False for k in range(4): ni nj = i + rowNum[k] j + colNum[k] if isValid(ni nj) and mat[ni][nj] == 0: return False return True # Pushing cells from the rightmost column into the queue for i in range(n): if check(i m - 1): q.append((i m - 1 1)) # BFS traversal while q: x y dis = q.popleft() if d[x][y] > dis: d[x][y] = dis for k in range(4): ni nj = x + rowNum[k] y + colNum[k] if check(ni nj): q.append((ni nj dis + 1)) # Finding the minimum distance in the first column ans = min(d[i][0] for i in range(n)) # If no safe path found return -1 if ans >= 10**9: ans = -1 return ans if __name__ == '__main__': mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ] result = findShortestPath(mat) print(result)
using System; using System.Collections.Generic; class Solution { static int[] rowNum = { -1 0 0 1 }; static int[] colNum = { 0 -1 1 0 }; // Check if cell is valid static bool IsValid(int i int j int n int m) { return !(i < 0 || i >= n || j < 0 || j >= m); } // Check if cell and its adjacent cells are safe static bool Check(int i int j int[][] mat int n int m) { if (!IsValid(i j n m)) return false; for (int k = 0; k < 4; k++) { int ni = i + rowNum[k]; int nj = j + colNum[k]; if (IsValid(ni nj n m) && mat[ni][nj] == 0) return false; } return true; } public static int FindShortestPath(int[][] mat) { int n = mat.Length; int m = mat[0].Length; Queue<(int int int)> q = new Queue<(int int int)>(); int[] d = new int[n m]; // Initialize distance array with large value for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) d[i j] = int.MaxValue / 2; // Push safe cells from rightmost column for (int i = 0; i < n; i++) { if (Check(i m - 1 mat n m)) { q.Enqueue((i m - 1 1)); } } // BFS traversal while (q.Count > 0) { var (x y dis) = q.Dequeue(); if (d[x y] > dis) { d[x y] = dis; for (int k = 0; k < 4; k++) { int ni = x + rowNum[k]; int nj = y + colNum[k]; if (Check(ni nj mat n m)) { q.Enqueue((ni nj dis + 1)); } } } } // Find minimum distance in the first column int ans = int.MaxValue / 2; for (int i = 0; i < n; i++) ans = Math.Min(ans d[i 0]); return ans >= int.MaxValue / 2 ? -1 : ans; } static void Main() { int[][] mat = new int[][] { new int[] {1 0 1 1 1} new int[] {1 1 1 1 1} new int[] {1 1 1 1 1} new int[] {1 1 1 0 1} new int[] {1 1 1 1 0} }; int result = FindShortestPath(mat); Console.WriteLine(result); } }
function findShortestPath(mat) { const n = mat.length; const m = mat[0].length; const rowNum = [-1 0 0 1]; const colNum = [0 -1 1 0]; // Distance matrix initialized to large value const d = Array.from({ length: n } () => Array(m).fill(Number.MAX_SAFE_INTEGER)); // Check if cell is valid function isValid(i j) { return !(i < 0 || i >= n || j < 0 || j >= m); } // Check if cell and its adjacent cells are safe function check(i j) { if (!isValid(i j)) return false; for (let k = 0; k < 4; k++) { let ni = i + rowNum[k]; let nj = j + colNum[k]; if (isValid(ni nj) && mat[ni][nj] === 0) return false; } return true; } // Queue for BFS let q = []; // Push safe cells from rightmost column for (let i = 0; i < n; i++) { if (check(i m - 1)) { q.push([i m - 1 1]); } } // BFS traversal while (q.length > 0) { let [x y dis] = q.shift(); if (d[x][y] > dis) { d[x][y] = dis; for (let k = 0; k < 4; k++) { let ni = x + rowNum[k]; let nj = y + colNum[k]; if (check(ni nj)) { q.push([ni nj dis + 1]); } } } } // Find minimum distance in first column let ans = Number.MAX_SAFE_INTEGER; for (let i = 0; i < n; i++) { ans = Math.min(ans d[i][0]); } return ans >= Number.MAX_SAFE_INTEGER ? -1 : ans; } const mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ]; const result = findShortestPath(mat); console.log(result);
Izlaz
6
Vremenska složenost: O(r * c) gdje su r i c broj redaka i stupaca u danoj matrici.
Pomoćni prostor: O(r * c)
