Stablo izraza je stablo koje se koristi za predstavljanje različitih izraza. Struktura podataka stabla koristi se za predstavljanje izraznih izjava. U ovom stablu unutarnji čvor uvijek označava operatore.
- Listni čvorovi uvijek označavaju operande.
- Operacije se uvijek izvode na ovim operandima.
- Operator prisutan u dubini stabla uvijek ima najveći prioritet.
- Operator koji nije mnogo dublje u stablu uvijek ima najniži prioritet u odnosu na operatore koji leže na dubini.
- Operand će uvijek biti prisutan na dubini stabla; stoga se smatra najveći prioritet među svim operaterima.
- Ukratko, možemo to sažeti kao vrijednost prisutna na dubini stabla najvišeg je prioriteta u usporedbi s drugim operatorima prisutnima na vrhu stabla.
- Glavna upotreba ovih izraznih stabala je da se koriste procijeniti, analizirati i modificirati razne izraze.
- Također se koristi za određivanje asocijativnosti svakog operatora u izrazu.
- Na primjer, operator + je lijevi asocijativ, a / je desni asocijativ.
- Dilema ove asocijativnosti razjašnjena je upotrebom izraza stabla.
- Ova izrazna stabla formirana su korištenjem gramatike bez konteksta.
- Povezali smo pravilo u gramatikama bez konteksta ispred svake gramatičke produkcije.
- Ta su pravila također poznata kao semantička pravila, a korištenjem tih semantičkih pravila možemo lako konstruirati stabla izraza.
- To je jedan od glavnih dijelova dizajna prevoditelja i pripada fazi semantičke analize.
- U ovoj semantičkoj analizi koristit ćemo prijevode usmjerene na sintaksu, au obliku izlaza proizvest ćemo označeno stablo raščlanjivanja.
- Anotirano stablo raščlanjivanja nije ništa drugo nego jednostavno raščlanjivanje povezano s atributom tipa i svakim proizvodnim pravilom.
- Glavni cilj korištenja stabala izraza je izrada složenih izraza i može se lako procijeniti pomoću ovih stabala izraza.
- Ono je nepromjenjivo i nakon što smo kreirali stablo izraza, ne možemo ga mijenjati niti dalje modificirati.
- Da biste izvršili više izmjena, potrebno je u cijelosti konstruirati novo stablo izraza.
- Također se koristi za rješavanje procjene izraza postfiksa, prefiksa i infiksa.
Stabla izraza igraju vrlo važnu ulogu u predstavljanju jezična razina kod u obliku podataka, koji su uglavnom pohranjeni u strukturi stabla. Također se koristi u prikazu memorije lambda izraz. Koristeći strukturu podataka stabla, možemo izraziti lambda izraz transparentnije i eksplicitnije. Prvo se stvara za pretvaranje segmenta koda u segment podataka tako da se izraz može lako procijeniti.
Stablo izraza je binarno stablo u kojem svaki vanjski ili listni čvor odgovara operandu, a svaki unutarnji ili nadređeni čvor odgovara operatorima, tako da bi na primjer stablo izraza za 7 + ((1+8)*3) bilo:
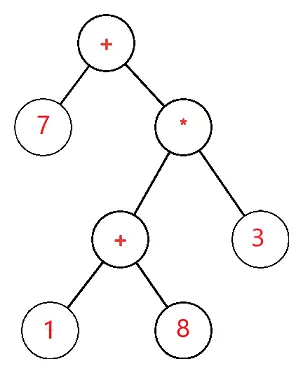
Neka je S stablo izraza
Ako S nije nula, tada
Ako je S.vrijednost operand, tada
Povratak S.vrijednost
x = riješiti (S.lijevo)
y = riješiti (S.desno)
Povratni izračun (x, y, S.vrijednost)
Ovdje u gornjem primjeru stablo izraza koristilo je gramatiku bez konteksta.
Imamo neke produkcije povezane s nekim proizvodnim pravilima u ovoj gramatici, uglavnom poznate kao semantička pravila . Možemo definirati stvaranje rezultata iz odgovarajućih pravila proizvodnje pomoću ovih semantičkih pravila. Ovdje smo upotrijebili parametar vrijednosti koji će izračunati rezultat i vratiti ga na početni simbol gramatike. S.left će izračunati lijevo dijete čvora, a slično tome, desno dijete čvora može se izračunati pomoću parametra S.right.
Korištenje izraznog stabla
- Glavni cilj korištenja stabala izraza je izrada složenih izraza i može se lako procijeniti pomoću ovih stabala izraza.
- Također se koristi za određivanje asocijativnosti svakog operatora u izrazu.
- Također se koristi za rješavanje procjene izraza postfiksa, prefiksa i infiksa.
Implementacija stabla izraza
Da bismo implementirali stablo izraza i napisali njegov program, morat ćemo koristiti strukturu podataka stog.
Kako znamo da se stog temelji na LIFO principu zadnji ušao prvi izašao, podatkovni element koji je nedavno gurnut u stog je iskočio kad god je to bilo potrebno. Za njegovu implementaciju koriste se dvije glavne operacije steka, push i pop. Operacijom push gurnut ćemo element podataka u stog, a operacijom pop ukloniti element podataka sa stoga.
Glavne funkcije stoga u implementaciji stabla izraza:
Prije svega, napravit ćemo skeniranje zadanog izraza na način slijeva nadesno, zatim jedan po jedan provjeriti identificirani znak,
- Ako je skenirani znak operand, primijenit ćemo operaciju push i gurnuti ga u stog.
- Ako je skenirani znak operator, primijenit ćemo operaciju pop na njega da uklonimo dvije vrijednosti sa stoga kako bismo ih učinili njegovim podređenim, a nakon toga ćemo vratiti trenutni roditeljski čvor u stog.
Implementacija Expression stabla u C programskom jeziku
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Izlaz gornjeg programa je:
X + Y * Z / W
Implementacija Expression stabla u C++ programskom jeziku
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Izlaz gornjeg programa je:
X + Y * Z / W
Implementacija Expression stabla u programskom jeziku Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 