- DFA se odnosi na determinističke konačne automate. Deterministički se odnosi na jedinstvenost izračuna. Konačni automati nazivaju se deterministički konačni automati ako stroj čita ulazni niz simbol po simbol.
- U DFA-u postoji samo jedan put za određeni unos iz trenutnog stanja u sljedeće stanje.
- DFA ne prihvaća nulti potez, tj. DFA ne može promijeniti stanje bez bilo kakvog ulaznog znaka.
- DFA može sadržavati više konačnih stanja. Koristi se u leksičkoj analizi u prevoditelju.
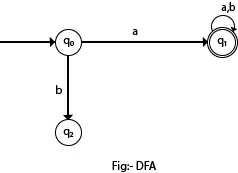
Na sljedećem dijagramu možemo vidjeti da od stanja q0 za ulaz a postoji samo jedan put koji vodi do q1. Slično, od q0, postoji samo jedan put za ulaz b koji ide do q2.
Formalna definicija DFA
DFA je kolekcija 5-torki isto kao što smo opisali u definiciji FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Prijelazna funkcija može se definirati kao:
δ: Q x ∑→Q
Grafički prikaz DFA
DFA se može prikazati digrafovima koji se nazivaju dijagrami stanja. U kojem:
- Stanje je predstavljeno vrhovima.
- Luk označen ulaznim znakom prikazuje prijelaze.
- Početno stanje je označeno strelicom.
- Konačno stanje je označeno dvostrukim krugom.
Primjer 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Riješenje:
Dijagram prijelaza:

Prijelazna tablica:
| Sadašnje stanje | Sljedeće stanje za ulaz 0 | Sljedeće stanje unosa 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Primjer 2:
DFA s ∑ = {0, 1} prihvaća sve koje počinju s 0.
Riješenje:

Obrazloženje:
- U gornjem dijagramu možemo vidjeti da na dan 0 kao ulaz u DFA u stanju q0, DFA mijenja stanje u q1 i uvijek ide u konačno stanje q1 na početnom unosu 0. Može prihvatiti 00, 01, 000, 001... itd. Ne može prihvatiti nijedan niz koji počinje s 1, jer nikada neće ići u konačno stanje na nizu koji počinje s 1.
Primjer 3:
DFA s ∑ = {0, 1} prihvaća sve koji završavaju s 0.
Riješenje:

Obrazloženje:
Na gornjem dijagramu možemo vidjeti da na dana 0 kao ulaz u DFA u stanju q0, DFA mijenja stanje u q1. Može prihvatiti bilo koji niz koji završava s 0, poput 00, 10, 110, 100... itd. Ne može prihvatiti niti jedan niz koji završava s 1, jer nikada neće prijeći u konačno stanje q1 na 1 ulazu, tako da niz koji završava s 1, neće biti prihvaćen ili će biti odbijen.
